基本介紹
中心射影
在平面上任取兩條相交的直線a和a’(圖1),並且在兩條直線外任取—點S,在直線a上取一點A,通過點S和點A引直線SA,設它與直線a'交於A',則點A'叫做直線a上的點A在a'上的中心射影,點S叫做射影中心,直線SA叫做投射線 。
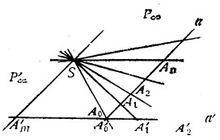 圖1
圖1如果在直線a上取點A,A,……則用上述方法在直線a'上可以得到它們的射影A',A',……。
由點A,A,……求它們射影A',A',……的作法,叫做 中心射影法。
從中心射影的定義,我們看出,如果A'是直線a上點A在直線a'上的射影,則A也是直線a'上點A'在直線a上的射影,一般來說對於直線a(或a’)上的一個點A(或A')總可以找到它在直線a'(或a)上的射影A'(或A)。但是我們看出,在歐幾里得平面上使用中心射影法將遇到困難,這就是直線a上的點在直線a'上不一定都有射影,同時直線a'上的點也可能不是直線a上任何點的射影。換句話說就是點與它的射影之間不能作成一一對應。
例如,在直線a上取點A使投射線SA平行於a',由於在歐幾里得平面上平行線不相交,所以它在直線a'上沒有射影。同樣,如果在直線a'上取點A',使投射線SA'平行於直線a,則它也不是直線a上任何點的射影。
因此,在歐幾里得平面上利用中心射影法所建立的點之間的對應不是一對一的;如果不消除這個缺點,則套用中心射影法研究問題就有很大的障礙,因此,我們有必要對歐幾里得平面進行某種改造,使改造後的平面,可以套用中心射影法建立點與它的射影之間的一一對應,而沒有任何例外 。
無窮遠元素的引入
我們將要建立的射影變換,必須是元素間一一的對應,而且要把直線變成直線,這樣才能包括仿射和正交變換,但是在歐氏平面上直線和直線之間在中心射影下不能建立點的一一對應,這就使我們遇到了很大的障礙,因此必須對歐氏平面進行拓廣,使它成為一種新的平面,在這個平面上,利用中心射影法,能夠使直線和直線間的點建立一一對應,究竟怎樣對歐氏平面加以拓廣呢?這就是引進無窮遠元素.我們約定 :
約定1 所有的在同一方向上平行的直線族,相交於同一個點,這個點叫做無窮遠點或理想點,用A、B等表示。
根據這一約定,在不同方向上的平行直線族必然交於不同的無窮遠點,否則兩組不同的平行線將成為在同一方向上平行的直線,這與已知矛盾。因為平面上的直線可有無窮多個方向,因此,平面上將有無窮多個無窮遠點。
約定2 平面上所有無窮遠點的集合組成一條直線,這條直線叫做無窮遠直線,用a、b等表示。
無窮遠直線實際是三維空間中平行平面的交線。
這樣,我們就在每一個歐氏直線上添加了一個無窮遠點,在每一個歐氏平面上添加了一條無窮遠直線。
定義 增加了無窮遠點的直線叫做 射影直線,增加了無窮遠直線的平面叫做 射影平面。
我們還可以定義 三維的射影空間。那就是增加第三個約定。
 三維射影空間
三維射影空間約定3 空間內一切無窮遠點的集合組成一個平面,這個平面叫做無窮遠平面。常用 來表示。
定義 增加了無窮遠平面的空間叫做 射影空間。
要注意,這兩個定義里提到的新增加的無窮遠元素與原來的元素(或叫有窮元素、
固有元素)的地位是完全相同,兩者不應加以區分給以不同的對待,如果把無窮遠點,直線或平面與原有的點,直線或平面加以區分,把無窮遠元素看成是特定的元素來對待,這樣的直線、平面和空間就是仿射的直線、平面或空間,這時把兩條交於無窮遠點的直線稱為平行線,等等。
 三維射影空間
三維射影空間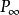 三維射影空間
三維射影空間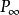 三維射影空間
三維射影空間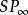 三維射影空間
三維射影空間現在我們再回過頭去看圖1,由於引進了無窮遠點,直線a上的A點將對應直線a'上的無窮遠點 ,這是因為直線SA平行於a';而直線a上的無窮遠點 將對應直線a'上的A',這是因為a上的也是直線SA'上的無窮遠點,而與a'交於A'這樣,直線a與直線a'在以S為中心的中心射影下建立了點間的一一對應。不僅如此,這時以S為中心的線束與直線a上的點(或a'上的點)也建立了一一對應的關係,即直線SA對應於點A,這兩個對應是一維基本形間的一種透視對應,從這個對應關係中還看出,無窮遠點可以與有窮遠點互相對應。
如果把無窮遠元素特殊對待,以無窮遠點為中心的中心射影就變成平行射影,這時所有投射線平行。
在推廣了的平面上,“平行”與“相交”兩個概念得到了統一,點和直線在結合關係上取得了對等的地位 。
空間中的射影坐標
我們從擴充空間加以一般化,排除正常點與無窮遠點的區分,即得出一般射影空間(或三維射影空間)概念。
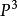 三維射影空間
三維射影空間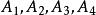 三維射影空間
三維射影空間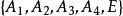 三維射影空間
三維射影空間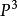 三維射影空間
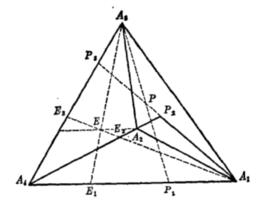
三維射影空間在三維射影空間中取不共面的四點以及不在這四點所決定的四面體的面上的任一點E,由這五點所構成的系統稱為中的一個 射影坐標系 。
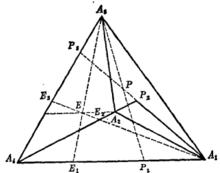 圖2
圖2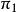 三維射影空間
三維射影空間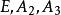 三維射影空間
三維射影空間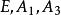 三維射影空間
三維射影空間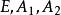 三維射影空間
三維射影空間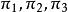 三維射影空間
三維射影空間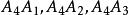 三維射影空間
三維射影空間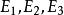 三維射影空間
三維射影空間我們用表示由點所決定的平面,用π表示由點所決定的平面,而且用π表示由點所決定的平面,這三個平面與分別交於點。
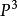 三維射影空間
三維射影空間對射影空間中任意一點P,用P表示平面PAA與AA的交點,用P表示平面PAA與AA的交點,用P表示平面PAA與AA的交點。令
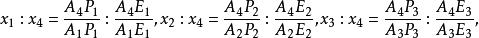 三維射影空間
三維射影空間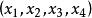 三維射影空間
三維射影空間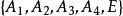 三維射影空間
三維射影空間則成比例的實數組稱為P點關於射影坐標系的 射影坐標。
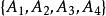 三維射影空間
三維射影空間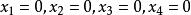 三維射影空間
三維射影空間這時四面體稱為 坐標四面體,E稱為 單位點;諸參考點的射影坐標分別為A(1,0,0,0), A(0,1,0, 0), A(0, 0,1, 0),A(0,0, 0,1), E(1,1,1, 1);四個坐標平面的方程分別為。
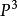 三維射影空間
三維射影空間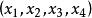 三維射影空間
三維射影空間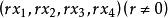 三維射影空間
三維射影空間因此可把三維射影空間看為點集,其點與不全為零的實數組建立對應,並規定凡成比例的實數組對立於同一點 。
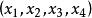 三維射影空間
三維射影空間現在寫出射影坐標與齊次坐標(x,y,z,t)之間的關係式,設坐標平面x=0(i=1,2, 3,4)關於齊次坐標的方程
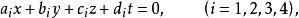 三維射影空間
三維射影空間則有
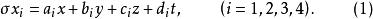 三維射影空間
三維射影空間由於四個平面不共點,所以
 三維射影空間
三維射影空間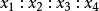 三維射影空間
三維射影空間反之,假定已知四個不全內零的數之比,則解方程組(1),得出
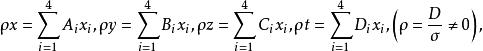 三維射影空間
三維射影空間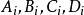 三維射影空間
三維射影空間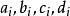 三維射影空間
三維射影空間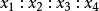 三維射影空間
三維射影空間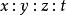 三維射影空間
三維射影空間式中為在行列式D中的代數餘子式。這表示與組成一個一一對立 。