概念
射影態射(projective morphism)是射影簇的推廣及相對化。設S是一個概形,Z上射影空間:
P=Proj Z[T,T,…,T]
用S→Spec Z做基擴張後可以得到S上的射影空間P=P×S。若態射f:X→S可以分解為一個閉浸入X→P以及投影P→S的複合,則稱f是射影態射,X稱為射影S概形。直觀地看,射影S概形就是S上某個射影空間的閉子概形。諾特概形的射影態射一定是正常態射。射影態射是一個整體概念,即射影態射f:X→S在任一點s∈S上的纖維f(s)都是剩餘域k(s)上的射影概形;但反之則不對。當S=Spec A是仿射概形時,射影S概形一定是某個分次A代數的齊次譜。當S是一般概形時,一定存在分次O代數層R,使得射影S概形同構於Proj R。
向量空間
設K為交換體。稱賦以由下列兩個給定法則所定義的代數結構的集合E為K上的向量空間:
——記為加法的合成法則,
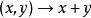 射影態射
射影態射——記為乘法的作用法則,即從K×E到E中的映射,
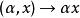 射影態射
射影態射這兩個法則滿足下列條件:
a)賦以加法的集合E是交換群;
b) 對K的任一元素偶(α,β),以及對E的任一元素x,
α(βx)=(αβ)x;
c) 對E的任一向量x,1x=x,其中1表示體K的單位元素;
d)對K的任一元素偶(α,β),以及對E的任一元素偶(x,y),
(α+β)x=αx+βx
α(x+y)=αx+αy.
當體K不再假定為交換的時,滿足上述條件的集合E稱為K上的左向量空間。
如果條件α(βx)=(αβ)x換為α(βx)=(βα)x,則稱E為K上的右向量空間。
射影空間
射影空間是整體幾何最基本的研究對象之一。射影空間的概念最初產生於古典射影幾何。對於射影定理中的奇異情形(即有些直線相互平行的情形),為方便起見引入無窮遠點的概念,即規定平面上每條直線上有一個無窮遠點,兩條直線平行就是相交於無窮遠點,所有無窮遠點組成一條無窮遠直線。這種構造方法還可以推廣到高維空間,建立n維(實)射影空間P。在n維射影空間中常採用齊次坐標(X∶X∶…∶X),其中X,X,…,X不全為0;若a≠0,則(aX∶aX∶…∶aX)與(X∶X∶…∶X)表示同一個點。因此n維(實)射影空間同構於(R-{0})/R。進一步的研究表明P是緊緻解析流形。若令U(0≤i≤n)為P中坐標X≠0的點全體,則UR,且U,U,…,U組成P的一個開覆蓋。上述構造方法可以推廣到任意體K上,建立K上的n維射影空間P。在概形理論中,還將射影空間建立在整數環Z上,即建立射影概形P。由此對任意概形X可以建立P,它是X和P(在Spec Z上)的纖維積。特別地,若X=Spec K(K為域),則P=Pn。
由於射影空間的性質非常豐富難以全面列舉,僅舉數例如下:
1.P同胚於圓,P可看做添上無窮遠點的複平面,同胚於球面.
2.P是單側曲面,可以同胚地嵌入四維空間R,但不能同胚地嵌入三維空間R,P是代數極小曲面.
3.P是克勒流形,它的閉解析子空間都是代數的.
4.對任意域k,P是齊性空間,其切叢由整體向量場生成,其自同構群為射影群PSL(n+1,k),其皮卡群Pic(P)Z。
射影簇
設P(E)為由向量空間E導出的射影空間。對E的任一向量子空間E′,在典範映射π下,E′-{0}的象叫做射影線性簇,射影簇或射影子空間,並記為P(E′)。
概形
概形是代數幾何的基本研究對象。它實際上就是一個局部同構於仿射概形的局部環空間。更精確地,概形(X,O)是一個環空間,其拓撲空間X有一個開覆蓋{X},使得(X,O|X)同構於仿射概形Spec Γ(X,O)(這樣的覆蓋稱為仿射開覆蓋)。概形間的態射就是局部環空間的態射。概形的範疇是局部環空間範疇的子範疇。若概形X有一個仿射開覆蓋{X},使得每個仿射概形都是諾特概形、既約概形、正規概形或正則概形,則相應地稱概形X是局部諾特的、既約的、正規的或正則的。這些性質都是概形的局部性質,就是說,只要存在一個仿射開覆蓋具有上述某種性質,這個概形就具有此性質,而且任意一個仿射開子概形都有此性質.若概形X的拓撲空間是連通空間或不可約空間(即它不能表成兩個不同真閉子集的並),則稱此概形為連通的或不可約的。
在研究概形的性質或有關的概念時,往往要考慮具有相同基礎的概形。帶有態射f:X→S的概形X稱為S概形.若S=Spec A是仿射概形,則S概形簡稱A概形。顯然任何概形都是Z概形。給出基變換態射S′→S後,可以得到一個S′概形X=X×S′,稱為S概形X的基擴張.與S概形相關的概念稱為相對概念,以區別於與概形相關的絕對概念。S概形與態射f:X→S密切相關.不同性質的態射就給出了不同的S概形。例如,設f:X→S是一個態射,若對角浸入X→X×X是閉態射,則稱f是分離態射;若存在S的一個仿射開覆蓋{U}={Spec B},使得每個f(U)都有一個有限仿射開覆蓋{V}={Spec A},並且A都是有限生成B代數,則稱f是有限型的;若f(U)=Spec A,A都是有限生成B模,則稱f是有限態射。有限態射是仿射態射。代數幾何中研究的S概形一般都是分離、有限型的。
