實驗數據的誤差處理
正文
物理實驗的觀測值都有誤差，從而使實驗結果帶有不確定性。實驗數據誤差處理的目的是估計實驗結果不確定性的大小，即估計實驗結果的精度。實驗誤差包括系統誤差和隨機誤差這兩類性質不同的誤差。由於實驗條件不正常或觀測者不小心而導致歪曲測量結果的過失誤差應當從測量中排除。系統誤差 是在一定的實驗條件下具有固定數值的誤差。判斷系統誤差的存在及其來源的方法主要有：①變化可能形成系統誤差的實驗條件，並比較不同條件下的測量結果；②對測得的數據進行統計假設檢驗（見數據的統計處理方法），以判斷觀測值的分布是否與隨機誤差的預期分布一致。
實驗前，應儘可能地消除導致系統誤差的因素，在多次觀測中，適當地改變產生系統誤差的實驗條件（如將條件對稱地或隨機地配置，使結果中的系統誤差相互抵消），有可能減少或消除最終結果中的系統誤差，已經判明的系統誤差數值應從測量結果中扣除。
隨機誤差 是由於測量的偶然誤差或被研究的物理現象本身的隨機性質所引起的觀測結果的不確定性。在一定的實驗條件下重複測量某一個物理量的數值，各次測量會得到不同的結果：觀測值服從某種統計分布，觀測值的分布愈寬，則從一次實驗得到的一個特定觀測值的不確定性愈大，即隨機誤差愈大，誤差理論的主要內容是如何估計實驗觀測結果的隨機誤差。
把通過實驗觀測得到某物理量θ的估計值記為
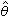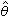,觀測結果 的精度可以用在某個給定的置信水平 ξ下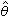附近的一個誤差區間，即置信區間,
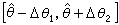來表示，或者寫作 
。
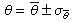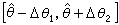中包含被測物理量真值θ的機率為ξ:如果在相同的實驗條件下重複多次觀測，由此得出多個不同的置信區間,則平均有份額為ξ的區間包含有被測物理量的真值，顯然，在一定的置信水平下，置信區間愈小則實驗結果的誤差愈小，結果愈精密。 常用標準誤差(分布方差的二次方根)表征一個統計分布的寬度,測量的偶然誤差大多服從常態分配,若物理量θ的觀測值服從標準誤差為σ的常態分配，觀測值中不包含系統誤差，觀測值分布的期待值(平均值)為被測物理量的真值θ,則對於一個觀測值θ
,區間
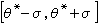的置信水平為68.3％，通常略去“置信水平68.3％”這句話而將結果簡單地記作 
。
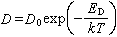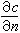也服從期待值為被測其值θ的常態分配，其標準誤差為
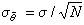，則將觀測結果記為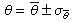
置信區間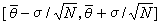 
的置信水平為68.3％，若標準誤差σ未知,需要由觀測值來估計，則可用
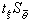表示估計值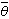
的誤差,置信區間的置信水平為ξ，或記作
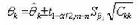
其中
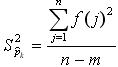實驗數據的誤差處理係數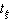
的數值由自由度N-1的t分布表查出，在測得數據較多時，如N>10，
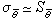,可以簡單地採用S
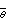作為觀測結果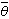的標準誤差。
若對於同一個物理量θ有N個不同精度的正態觀測結果θ1,θ2,…,θN，它們的標準誤差分別為σ1,σ2,…,σN，可採用加權平均值
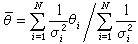
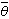服從常態分配，其標準誤差為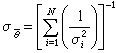 
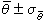的置信水平是68.3％。 在同時測量多個物理量的情況下，測量結果的精度由對於所有被測物理量的一個置信區域來表示，在一定的置信水平下，置信區域的大小和形狀不但同各個觀測值的誤差有關，而且與它們之間的相關程度有關。
已知直接觀測值的誤差，如何估計通過計算得到的間接觀測值的誤差，叫做誤差傳播問題，如果直接觀測值服從常態分配，而且間接觀測值是直接觀測值的線性函式，則間接觀測值也服從常態分配，其標準誤差可以用簡單的誤差傳播公式由直接觀測值的誤差算出，一般函式的誤差傳播問題，只有在各直接觀測值的誤差都較小的條件下，才可以近似地使用誤差傳播公式。很多實驗觀測結果（如一般情況下的間接觀測值）並不服從常態分配。在測量結果的不確定性主要由被研究的物理現象本身的隨機性質所決定的場合，觀測值一般也不服從常態分配，早期的物理實驗中，對於不服從常態分配的觀測值也採用其標準誤差表徵實驗結果的精度。這種情況下，相應誤差區間的置信水平並不是68.3％，而同觀測值分布的具體形式有關。在觀測值不服從常態分配的一般情況下，要想在確定的機率意義下表示實驗結果的誤差，即對於一定的置信水平求得相應的置信區間，必須套用數理統計學參量估計的方法（見數據的統計處理方法）。
參考書目
李惕碚著：《實驗的數學處理》，科學出版社，北京，1980。
