定義
天文導航的定義：根據天體來測定飛行器位置和航向的航行技術。天體的坐標位置和它的運動規律是已知的，測量天體相對於飛行器參考基準面的高度角和方位角就可以計算出飛行器的位置和航向。天文導航系統是自主式系統，不需要地面設備，不受人工或自然形成的電磁場的干擾，不向外輻射電磁波，隱蔽性好，定向、定位精度高，定位誤差與時間無關，因而天文導航得到廣泛套用。
原理
航空和航天的天文導航都是在航海天文導航基礎上發展起來的。航空天文導航跟蹤的天體主要是亮度較強的恆星。航天中則要用到亮度較弱的恆星或其他天體。以天體作為參考點，可確定飛行器在空中的真航向。使星體跟蹤器中的望遠鏡自動對準天體方向可以測出飛行器前進方向（縱軸）與天體方向（即望遠鏡軸線方向）之間的夾角（稱為航向角）。由於天體在任一瞬間相對於南北子午線之間的夾角（即天體方位角）是已知的。這樣，從天體方位角中減去航向角就得到飛行器的真航向。通過測量天體相對於飛行器參考面的高度就可以判定飛行器的位置。以地平坐標系在飛行器上測得某星體C的高度角h,由90°-h可得天頂距z（圖1），以星下點(天體在地球上的投影點)為圓心，以天頂距z所對應的地球球面距離R為半徑作一圓，稱為等高圓(圖2)。在這個圓上測得的天體高度角都是h。同時測量兩個天體C1、C2,便得到兩個等高圓。由這兩個圓的交點得出飛行器的實際位置M和虛假位置M′。再用飛行器位置的先驗信息或第三個等高圓來排除虛假位置，經計算機解算即得出飛行器所在的經、緯度(λ、φ)。
天文導航分類
根據跟蹤的星體數，天文導航分為單星、雙星和三星導航。單星導航由於航向基準誤差大而定位精度低，雙星導航定位精度高，在選擇星對時，兩顆星體的方位角差越接近90°，定位精度越高。三星導航常利用第三顆星的測量來檢查前兩次測量的可靠性，在航天中，則用來確定太空飛行器在三維空間中的位置。
儀器和系統
航空常用的天文導航儀器有星體跟蹤器、天文羅盤和六分儀等。自動星體跟蹤器自動星體跟蹤器(星敏感器)能從天空背景中搜尋、識別和跟蹤星體，並測出跟蹤器瞄準線相對於參考坐標系的角度。天文羅盤通過測量太陽或星體方向來指示飛行器的航向。六分儀通過對恆星或行星的測量而指示出飛行器的位置和距離。天文導航系統通常由星體跟蹤器、慣性平台、計算機、信息處理電子設備和標準時間發生器等組成。星體跟蹤器是天文導航系統的主要設備，一般由光學望遠鏡系統、星體掃描裝置、星體輻射探測器、星體跟蹤器信號處理電路和驅動機構等組成（圖3）。它通過掃描對星體進行搜尋，搜尋到星體之後立即轉入跟蹤狀態，同時測出星體的高度角和方位角。星體跟蹤器的輻射探測器在飛機上較多採用光電倍增管和光導攝像管，在太空飛行器上較多採用光導攝像管和析像管。電荷耦合器件是70年代發展起來的一種探測器，它體積小、靈敏度高、壽命長，不用高壓供電,能直接獲得精確的空間信息，近年來在飛機、飛彈、太空梭和衛星上得到廣泛套用，並為星體跟蹤器小型化創造了條件。
發展簡況
中國古籍有很多關於將天文套用於航海的記載。西漢《淮南子·齊俗訓》：“夫乘舟而惑者，不知東西,見斗極則寤矣。”東晉法顯《佛國記》:“大海瀰漫無邊，不知東西，唯望日月星辰而進。”北宋朱彧《萍洲可談》：“舟師識地理，夜則觀星，晝則觀日，陰晦觀指南針。”明《武備志》所收的《過洋牽星圖》記有南北、東西星體在水天線上若干指（角度單位）的數據，用以估計船位。
歐洲在15世紀以前僅能白晝順風沿岸航行。15世紀出現了用北極星高度或太陽中天高度求緯度的方法。當時只能先南北向駛到目的地的緯度，再東西向駛抵目的地。16世紀雖然已有觀測月距（月星之間角距）求經度法，但不夠準確，而且解算繁冗。18世紀六分儀和天文鐘先後問世，前者用於觀測天體高度，大大提高了準確性；後者可以在海上用時間法求經度。1837年美國船長T.H.薩姆納發現天文船位線，從此可以在海上同時測定船位的經度和緯度，奠定了近代天文定位的基礎。1875年法國海軍軍官聖伊萊爾發明截距法，簡化了天文定位線測定作業，至今仍在套用。
套用
天文導航經常與慣性導航、都卜勒導航系統組成組合導航系統。這種組合式導航系統有很高的導航精度，適用於大型高空遠程飛機和戰略飛彈的導航。把星體跟蹤器固定在慣性平台上並組成天文－慣性導航系統時，可為慣性導航系統的狀態提供最優估計和進行補償，從而使得一個中等精度和低成本的慣性導航系統能夠輸出高精度的導航參數。
在低空飛行時因受能見度的限制較少採用天文導航，但對於高空遠程轟炸機、運輸機和偵察機作跨越海洋、通過極地、沙漠上空的飛行，天文導航則很適用。對於遠程彈道飛彈，天文導航能修正發射點的初始位置和瞄準角誤差，所以特別適用於機動發射的飛彈。彈道飛彈可在主動飛行段的後期使用天文導航，也可借天文導航完成再入後的末制導用以修正風的影響。星體跟蹤器對星體的瞄準能建立精確的幾何參考坐標，並且在空間沒有雲的干擾，因而天文導航（星光制導）在太空飛行器上得到更廣泛的套用。
參考書目
王裕齊、申功勳編譯：《天文導航》，國防工業出版社，北京，1966。
天文航海的定義：在海上觀測天體確定船位的技術，又稱天文導航、航海天文學。
天文定位原理和方法
天文定位的基本問題就是通過觀測天體高度求得天文船位線。按照天球和地球的對應關係，被測天體在觀測時刻所對應的地理位置，即天體向地心投影的地麵點,稱為星下點(S)。天體星下點的經度和緯度分別等於該天體在觀測時刻的格林時角和赤緯，二者均可根據觀測時間從航海天文歷查得。觀測所得天體高度(h)的補角為天體頂距(z)，即：
z＝90°-h
觀測時的測者必定位於以星下點為中心，以天體頂距在地面所跨距離（一角度分相當於1海里）為半徑的圓上，這個圓稱天文船位圓，又稱等高圓。觀測兩個不同天體可得兩個天文船位圓，兩圓相交，靠近推算船位的交點就是天文船位（圖1）。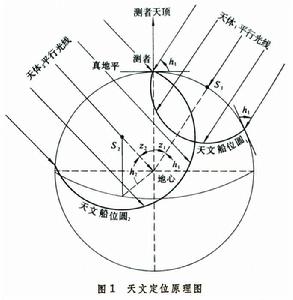 
天文船位圓一般很大，對定位有用的僅是靠近推算船位的在實用上可視為直線的小弧段，稱為天文船位線，又稱薩姆納線。通常在晨昏蒙影時間內同時觀測兩個以上星體求得天文船位線相交點定位;或在白天間隔一定時間（一般為2～3小時）觀測太陽求得天文船位線,按照航向和航程移線相交定位。航海者常將上午的太陽船位線移線與觀測太陽中天高度求得的緯度線相交得出中午天文船位。
天文船位線的求法一般是求解由天頂、天極、天體三點構成的球面三角形（稱為天文三角形）。天文三角形的解法有經度法和截距法，前者曾流行於19世紀，現已讓位於後者。
截距法是利用推算船位求出觀測和計算高度之差來畫天文船位線的方法，又稱高度差法或高度法。其步驟是：①用推算船位所對應的天頂解天文三角形求得天體計算高度和方位,精度分別要求達到0.1′和0.1°。②觀測高度減計算高度得截距，即得推算船位至天文船位圓的距離。截距為“+”,即推算船位在天文船位圓之外，說明天文船位線處於推算船位向著天體（星下點）的方向。截距為“-”,天文船位線處於背向天體的方向。③根據截距的符號和大小在天體計算方位線上量取截點，即可垂直畫出天文船位線。圖2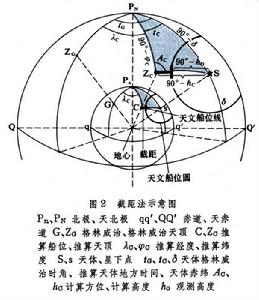
中觀測高度大於計算高度，截距為“＋”，應從推算船位向著天體畫天文船位線。實際上用以解天文三角形的推算點經、緯度在實用範圍內可以任選，不影響定位準確性。基本計算公式如下：
sinhc＝sin嗘csinδ+cos嗘ccosδcostc
ctgAc＝tgδcos嗘ccsctc-sin嗘cctgtc
或 sinAc＝sintccosδsechc （先解算hC）
式中嗘c、δ、tc分別為推算緯度、天體赤緯、天體地方時角(用推算經度)；hc、Ac分別為天體計算高度、計算方位。為簡化用截距法解天文三角形的數學演算，可套用天體高度方位表查取天體計算高度和方位。
觀測南北方向（中天）天體所得的緯度線為特殊的天文船位線，它的公式簡化為以下代數式：
天文船位誤差 取決於天文船位線的誤差及其方位夾角。船位誤差中有偶然誤差也有系統誤差。船位偶然誤差以誤差橢圓方法表示較為準確，但用均方誤差圓方法表示較方便。對兩條等精度天文船位線：
天文船位均方誤差圓半徑（63％～68％機率）＝
式中m、e分別為船位線的偶然誤差和系統誤差；A1、A2為兩天體方位。兩式中，天體方位夾角的影響正好相反。如m和e為同數量級，為了兼顧這兩種影響，兩天體方位夾角取 60°～70°最好，避免小於30°或大於150°。增加觀測天體的次數取均值，可提高定位的精確性。如果觀測三四個天體，它們的方位以分別相距 120°和90°為最好。這樣也便於消除系統誤差。有經驗的航海者在良好條件下測天定位的誤差很少超過2海里。
截距法
截距法簡介
天文船位線的求法一般是求解由天頂、天極、天體三點構成的球面三角形（稱為天文三角形）。天文三角形的解法有經度法和截距法，前者曾流行於19世紀，現已讓位於後者。
截距法是利用推算船位求出觀測和計算高度之差來畫天文船位線的方法，又稱高度差法或高度法。
截距法步驟
其步驟是：①用推算船位所對應的天頂解天文三角形求得天體計算高度和方位,精度分別要求達到0.1′和0.1°。②觀測高度減計算高度得截距，即得推算船位至天文船位圓的距離。截距為“+”，即推算船位在天文船位圓之外，說明天文船位線處於推算船位向著天體（星下點）的方向。截距為“-”,天文船位線處於背向天體的方向。③根據截距的符號和大小在天體計算方位線上量取截點，即可垂直畫出天文船位線。圖2中觀測高度大於計算高度，截距為“+”，應從推算船位向著天體畫天文船位線。實際上用以解天文三角形的推算點經、緯度在實用範圍內可以任選，不影響定位準確性。
基本計算公式
基本計算公式如下：
sinhc=sin嗘csinδ+cos嗘ccosδcostc
ctgAc=tgδcos嗘ccsctc-sin嗘cctgtc
或 sinAc=sintccosδsechc （先解算hC）
式中嗘c、δ、tc分別為推算緯度、天體赤緯、天體地方時角(用推算經度)；hc、Ac分別為天體計算高度、計算方位。為簡化用截距法解天文三角形的數學演算，可套用天體高度方位表查取天體計算高度和方位。
觀測南北方向（中天）天體所得的緯度線為特殊的天文船位線，它的公式簡化為以下代數式：
式中中天頂距命名與天體方向相反。頂距與赤緯同名相加，異名相減。緯度與大項同名。
天文船位誤差 取決於天文船位線的誤差及其方位夾角。船位誤差中有偶然誤差也有系統誤差。船位偶然誤差以誤差橢圓方法表示較為準確，但用均方誤差圓方法表示較方便。對兩條等精度天文船位線：
天文船位均方誤差圓半徑（63%～68%機率）=
式中m、e分別為船位線的偶然誤差和系統誤差；A1、A2為兩天體方位。兩式中，天體方位夾角的影響正好相反。如m和e為同數量級，為了兼顧這兩種影響，兩天體方位夾角取60°～70°最好，避免小於30°或大於150°。增加觀測天體的次數取均值，可提高定位的精確性。如果觀測三四個天體，它們的方位以分別相距120°和90°為最好。這樣也便於消除系統誤差。有經驗的航海者在良好條件下測天定位的誤差很少超過2海里。
展望
與無線電定位相比，天文定位受天氣條件限制，解算複雜費時，但卻有獨立性強，儀器簡單，費用節省，隱蔽性好，沒有覆蓋區限制，定位誤差穩定，沒有積累誤差等優點。目前天文定位正從如下幾方面改進：①實現定位計算全部自動化。各國已研製出多種航海計算器或天文定位計算器，有些已達到實現計算全部自動化的要求。②擴大晝夜觀測的時機。如40年代出現的幾種人工地平氣泡、陀螺六分儀，70年代前後出現的光增強夜視六分儀、晝夜數字六分儀、遙控微光電視照相六分儀、計算機六分儀等，但大部分仍處在完善或降低價格階段。③提高海上觀測的精度。如研究連續觀測高度、自動平差的儀器設備等。④開發天文定位的新途徑。如測定天體其他參數或其他的輻射波。20世紀50年代開始研製的射電六分儀，就是觀測天體的無線電波。⑤天文定位與其他導航儀聯合使用，取長補短。如已出現的組合導航系統。
參考書目
Nathaniel Bowditch, LL. D., American Practical Navigator, 1977 ed., Part Three, DMAHC, USA.
