基本簡介
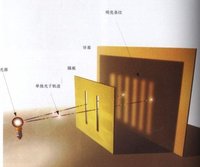
在雙縫實驗裡,照射單色光在一座有兩條狹縫的不透明擋牆。在擋牆的後面,設立了一個照相底片或某種偵測屏障,用來紀錄通過狹縫的光波的數據。從這些數據,可以了解光波的物理特性。以波動觀來解釋光波的干涉。
理察·費曼說:仔細地思考雙縫實驗的意義,我們就能夠一點一滴的了解整個量子力學。透過雙縫實驗,我們可以了解量子世界的真諦。
起源
 雙縫實驗
雙縫實驗托馬斯·楊(Thomas Young,1773—1829)於1801年進行了一次光的干涉實驗,即著名的楊氏雙孔干涉實驗,並首次肯定了光的波動性。隨後在他的論文中以干涉原理為基礎,建立了新的波動理論,並成功解釋了牛頓環,精確測定了波長。
1803年,楊把干涉原理用以解釋衍射現象。
1807年,楊發表了《自然哲學與機械學講義》(A course of Lecturse on Natural Philosophy and the Mechanical Arts),書中綜合整理了他在光學方面的理論與實驗方面的研究,
並描述了雙縫干涉實驗,後來的歷史證明,這個實驗完全可以躋身於物理學史上最經典的前五個實驗之列。但是他認為光是在以太媒質中傳播的縱波。這與光的偏振現象產生了矛盾,然而楊並未放棄光的波動說。
楊的著作點燃了革命的導火索,光的波動說在經過了百年的沉寂之後,終於又回到了歷史舞台上來。但是它當時的日子並不好過,在微粒說仍然一統天下的年代,楊的論文開始受盡了權威們的嘲笑和諷刺,被攻擊為“荒唐”和“不合邏輯”。在近20年間竟然無人問津,楊為了反駁專門撰寫了論文,但是卻無處發表,只好印成小冊子。但是據說發行後“只賣出了一本”。
1818年菲涅耳(Augustin Fresnel,1788—1827)在巴黎科學院舉行的一次以解釋衍射現象為內容的科學競賽中以光的干涉原理補充了惠更斯原理,提出了惠更斯-菲涅耳原理,完善了光的衍射理論並獲得優勝。早於1817年在面對波動說與光的偏振現象的矛盾時,楊覺察到如果光是橫波或許問題可以得到解決,並把這一想法寫信告訴了阿拉果(D.F.Arago,1786—1853),阿拉果立即把這一思想轉告給了菲涅耳。於是當時已獨自領悟到這一點的菲涅耳立即用這一假設解釋了偏振現象,證明了光的橫波特性,使得光的波動說進入一個新的時期。
理論依據
量子力學
 雙縫實驗
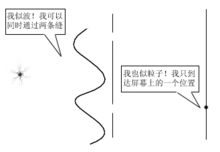
雙縫實驗讓我們考慮這一“原型的”量子力學實驗。一束電子或光或其他種類的“粒子-波”通過雙窄縫射到後面的螢幕去。為了確定起見,我們用光做實驗。按照通常的命名法,光量子稱為“光子”。光作為粒子(亦即光子)的呈現最清楚地發生在螢幕上。光以分立的定域性的能量單位到達那裡,這能量按照普朗克公式E=hv恆定地和頻率相關。螢幕從不會接收“半個”(或任何分數的)光子的能量
。光接收是以光子單位的完全有或完全沒有的現象。只有整數個光子才被觀察到。
然而,光子通過縫隙時似乎產生了類波動的行為。先假定只有一條縫是開的(另一條縫被堵住)。光通過該縫後就被散開來,這是被稱作光衍射的波動傳播的一個特徵。但是,這些對於粒子的圖像仍是成立的。可以想像縫隙的邊緣附近的某種影響使光子隨機地偏折到兩邊去。當相當強的光也就是大量的光子通過縫隙時,螢幕上的照度顯得非常均勻。但是如果降低光強度,則人們可斷定,其亮度分布的確是由單獨的斑點組成——和粒子圖像相一致——是單獨的光子打到螢幕上。亮度光滑的表觀是由於大量的光子參與的統計效應。(為了比較起見,一個60瓦的電燈泡每一秒鐘大約發射出10^20個光子!)光子在通過狹縫時的確被隨機地彎折——彎折角不同則機率不同,就這樣地得到了所觀察到的亮度分布。
然而,當我們打開另一條縫隙時就出現了粒子圖像的關鍵問題!假設光是來自於一個黃色的鈉燈,這樣它基本上具有純粹的非混合的顏色——用技術上的術語稱為單色的,也即具有確定的波長或頻率。在粒子圖像中,這表明所有光子具有同樣的能量。此處波長約為5×10-7米。假定縫隙的寬度約為0.001毫米,而且兩縫相距0.15毫米左右,螢幕大概在一米那么遠。在相當強的光源照射下,我們仍然得到了規則的亮度模式。但是我們在螢幕中心附近可看到大約三毫米寬的稱為干涉模式的條紋的波動形狀。我們也許會期望第二個縫隙的打開會簡單地把螢幕的光強加倍。如果我們考慮總的照度,這是對的。但是強度的模式的細節和單縫時完全不同。螢幕上的一些點——也就是模式在該處最亮處——照度為以前的四倍,而不僅僅是二倍。在另外的一些點——也就是模式在該處最暗處——光強為零。強度為零的點給粒子圖像帶來了最大的困惑。這些點是只有一條縫打開時粒子非常樂意來的地方。我們打開了另一條縫,忽然發現不知為什麼光子被防止跑到那裡去。我們讓光子通過另一條途徑時,怎么會在實際上變成它在任何一條途徑都通不過呢?
光的波動
在光子的情形下,如果我們取它的波長作為其“尺度”的度量,則第二條縫離開第一條縫大約有300倍“光子尺度”那么遠(每一條縫大約有兩個波長寬),這樣當光子通過一條縫時,它怎么會知道另一條縫是否被打開呢?事實上,對於“對消”或者“加強”現象的發生,兩條縫之間的距離在原則上沒有受到什麼限制。
當光通過縫隙時,它似乎像波動而不像粒子那樣行為。這種抵消——對消干涉——是波動的一個眾所周知的性質。原來兩條路徑的每一條分別都可讓光通過,而兩條同時都開放,則它們完全可能會相互抵消。這種現象發生的原因是:如果從一條縫隙來的一部分光和從另一條縫隙來的“同相”(也就是兩個部分波的波峰同時發生,波谷也同時發生),則它們將互相加強。但是如果它們剛好“反相”(也就是一個部分波的波峰重疊到另一部分的波谷上),則它們將互相抵消。在雙縫實驗中,只要螢幕上到兩縫隙的距離之差為波長的整數倍的地方,則波峰和波峰分別在一起發生,因而是亮的。如果距離差剛好是這些值的中間,則波峰就重疊到波谷上去,該處就是暗的。關於通常巨觀的經典波動同時以這種方式通過兩個縫隙沒有任何困惑之處。波動畢竟只是某種媒質(場)或者某種包含有無數很小點狀粒子的物體的一種“擾動”。擾動可以一部分通過一條縫隙,另一部分通過另一條縫隙。但是這裡的情況非常不同;每一個單獨光子自身是完整的波動!在某種意義上講,每個粒子一下通過兩條縫隙並且和自身干涉!人們可將光強降得足夠低使得保證任一時刻不會有多於一個光子通過縫隙的附近。對消干涉現象,因之使得兩個不同途徑的光子互相抵消其實現的可能性,是加在單獨光子之上的某種東西。如果兩個途徑之中只有一個開放,則光子就通過那個途徑。但是如果兩者都開放,則兩種可能性奇蹟般地互相抵消,而發現光子不能通過任一條縫隙!
實驗
實驗圖
 雙縫實驗
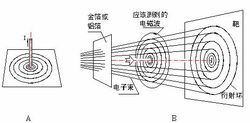
雙縫實驗做本實驗用的全部裝置如圖1所示,在可鏇轉式光具座導軌1的一端用滑塊固定光源2,光源燈泡由J1201型低壓電源的交流輸出供電,3是光源用單縫,縫寬0.11mm,光具架4裝在另一滑塊上,4中間安裝雙縫5,縫寬0.016~0.020mm,縫距0.080mm,導軌另一端用長滑塊固定。
6是觀察筒。各光具的光軸要和導軌平行並大致共軸.光源燈泡是“12V 50W”鹵鎢燈,為了延長它的壽命,開始先用6V點亮,避免很大的衝擊電流,然後根據實驗所需的亮度逐漸升高電壓,但不得超過12V
實驗前的調整:只裝上光源2,在導軌另一端裝毛玻璃屏,轉動光源,使射出的光束在屏的中央形成光斑.再裝上光源單縫、光具架和雙縫,單縫取豎直方向,雙縫外環上的指示線對準光具架上的零刻線,雙縫距離單縫5~10cm.此時順著光的傳播方向看,通過單縫的光形成的窄條形光斑應恰好落在雙縫上,如偏斜則應轉動光源和單縫使之對準.即單縫與雙縫平行.再取下毛玻璃屏.裝上觀察筒,對準光具架稍加轉動,就能由大透鏡看到筒內毛玻璃屏上呈現不少於5條的彩色干涉條紋.觀察筒入光口裝有可平移的方形光欄,用以擋住環境中的雜散光的干擾,使視場中的干涉條紋清晰可見.如果幹涉條紋形狀不好或不出現條紋,可能是單縫與雙縫不平行,再仔細調節即可.在光源上加濾色片,可看到近乎單色的明暗相間的干涉條紋,還可加不同顏色的玻璃,看到的干涉條紋間距離不同.使光源適當靠近雙縫可增加干涉明條紋的亮度,使明暗條紋反差增大.使觀察筒離雙縫遠些,干涉條紋間距離變大,但亮度要減弱.
這個實驗在不太亮的教室中就能進行,轉動光具座導軌,讓全班學生在座位上輪流觀察。
自製儀器
按圖2自製一個雙縫,e是一塊復銅絕緣板(或較厚的平整鐵片),按虛線挖一個長方孔,在復銅面上用錫焊牢一根直徑0.05~0.10mm的細銅絲ab,要繃直。再焊上兩個刮臉刀片c、d,刀片的刃要平直並且和銅絲平行,距離儘量近但勿接觸,形成的縫寬宜小於0.2mm,可在ab兩側先各貼放一根細漆包線,將刀片刃和漆包線貼緊,焊好後再取走漆包線。以上操作可在放大鏡下進行。
用平面鏡將日光反射到暗室中,先通過一個硬紙板做的單縫,縫寬約0.5mm,再投射到自製雙縫上,雙縫距單縫0.5~1m;在雙縫後1~2m的白牆上就呈現彩色干涉條紋。若在單縫前放三稜鏡將日光色散,使單縫通過某一顏色的光,則得到單色干涉條紋,但亮度弱,宜投在毛玻璃屏上由屏後觀察。
雷射光學
可得到真正的單色光的干涉圖樣.用氦氖雷射照射儀器所附的雙縫,可在不太亮的教室中幾米遠的白牆上形成間距相當大的干涉圖樣供全班同時觀看。因雷射束直徑很小,故形成的干涉條紋很短,近似為點狀。
原理
兩個相干光源干涉會產生干涉條紋,例如楊氏干涉兩相鄰直條紋的間距為△x=λl/d,其中d為兩個狹縫中心的間距,λ是單色光波波長,ι是雙縫屏到和它平行的考察屏的距離。菲涅耳(Fresnel)雙稜鏡以折射的方式分割由S發出的波陣面,其本質就是一個變樣的楊氏雙縫干涉,工作原理和楊氏雙縫干涉一樣。
內容步驟
光路調節
 雙縫實驗
雙縫實驗⑴將單色光源M、會聚透鏡L、狹縫S、雙稜鏡AB與測微目鏡P,按圖16-2所示次
序放置在光具座上,用目視粗略地調整它們中心等高、共軸,並使雙稜鏡的底面與系統的光軸垂直,棱脊和狹縫的取向大體平行。
⑵點亮光源M,通過透鏡照亮狹縫S,用手執白紙屏在雙稜鏡後面檢查;
干涉條紋
 雙縫實驗
雙縫實驗⑴減小狹縫寬度(以提高光源的空間相干性),一般情況下可從測微目鏡觀察到不太清晰的干涉條紋。
⑵繞系統光軸緩慢地向左或右鏇轉雙稜鏡B,當轉到雙稜鏡脊與狹縫的取向嚴格平行時,顯現出清晰的干涉條紋。
⑶為便於測量,在看到清晰的干涉條紋後,應將雙稜鏡或測微目鏡前後移動,使干涉條紋的寬度適當,同時只要不影響條紋的清晰度,可適當增加縫寬,以保持干涉條紋有足夠的亮度。
測量
在雙稜鏡和目鏡之間插放凸透鏡L,並調節L的位置和目鏡的位置,
使得從目鏡里能看到清晰的雙縫象。當這個象和分劃版上的叉絲之間無視差時,用測微目鏡量出雙縫象的間距do′再量出成象時的物距u(即狹縫S到透鏡L的距離)和象距v(即透鏡L到分劃版之間的距離),即可根據d=d’u/v算出兩個虛光源S1、S2的間距d。最後,可以根據DX、ι和d算得準單色光源的波長λ。
雙縫衍射
引言
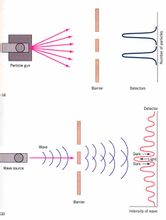
美國物理學家費曼曾說:在雙縫衍射現象中“包括了量子力學唯一的奧秘。”在他的名著《費曼物理學講義Ⅲ》一書的第一章中,以“量子行為”為標題,詳細考察了電子的雙縫衍射實驗的這個“奧秘”:如果電子槍發出一束電子通過兩條縫落在後面的螢幕上,則一方面落在螢幕上的電子呈現出像子彈一樣的顆粒性,另一方面螢幕上的電子的數目分布呈現出像水波一樣的干涉現象。電子的這種行為否定了如下命題:
A:在兩條縫同時打開的條件下的衍射圖形將是在兩條縫分別輪流打開的條件下得到的兩個衍射圖形的迭加。
費曼說:這種行為是“極其神秘”的,而且“你考慮的越多,就越會感到神秘。”他還說:人們曾經構想單個電子以各種複雜方式繞行通過縫來解釋這種行為,但都不成功。最後人們才認識到,導致命題A的是如下前提:
B:每一個達到螢幕的電子不是通過第一條縫就是通過第二條縫。
在《費曼物理學講義Ⅲ》一書中,未曾詳細表述如何從命題B導出命題A。根據後人的理解,這一推導過程可以表述如下:
第一步:按照命題B,如果在電子的雙縫衍射實驗中同時打開兩條縫,讓一束電子通過這兩條縫到達一個螢幕,則一個到達螢幕上的電子必須而且僅僅通過某一條縫。因此,如果用符號e表示一個到達螢幕的電子,E表示“e通過第一條縫”而F表示“e通過第二條縫”,則有:
 雙縫實驗
雙縫實驗E∪F=U (必然事件),E∩F=∅ (不可能事件)。⑴
第二步,令x表示屏上的一個小區域,X表示“e落在x上”,則E∩X表示“e通過第一條縫落在x上”;而F∩X表示“e通過第二條縫落在x上”。根據事件運算的布爾代數規則,從⑴式可得出:
E∩X∪F∩X=X,(E∩X)∩(F∩X)=∅。⑵
第三步,根據機率的頻率定義,從上述公式可得出:
Pr(X)=Pr(E∩X)+Pr(F∩X)。⑶
這是機率的加法公式的一種形式。
第四步,根據機率的乘法公式,有
Pr(E∩X)=Pr(E)Pr(X|E);Pr(F∩X)=Pr(F)Pr(X|F)。⑷
套用⑷式,⑶式表成
 雙縫衍射
雙縫衍射Pr(X)=Pr(E)Pr(X|E)+Pr(F)Pr(X|F)。⑸
nikantayande
這是機率論中的“全機率公式”。
如果只打開第一條縫,事件“e落在x上”的機率為Pr(X|E);如果只打開第二條縫,該事件的機率為Pr(X|F);如果兩條縫都打開,該事件的機率為Pr(X)。按照全機率公式,Pr(X)是Pr(X|E)和Pr(X|F)按照Pr(E)與Pr(F)的比例相加,特別是,當Pr(E)=Pr(F)=1/2時,Pr(X)是Pr(X|E)和Pr(X|F)的算術平均值。考慮到x是螢幕上的任意區域,由此立刻得出命題A。但雙縫衍射實驗否定了這一結論。於是費曼得出必須放棄命題B的結論。
如果電子的運動是軌道運動,則命題B肯定成立,因此費曼實際上斷言:“電子的運動不是軌道運動。”這正是哥本哈根詮釋的基本觀點。
從數學的角度來看,命題A是⑸式的結論,而⑸式則是根據⑴式、⑵式、⑶式和⑷式一步步導出的。我們看到,為了擺脫命題A與實驗事實之間的矛盾,費曼的思路是:否定命題B,從而否定了⑴式,從而得不到命題A,從而導致量子力學的哥本哈根詮釋。
其它詮釋
 雙縫實驗示意圖
雙縫實驗示意圖同樣為了擺脫命題A與實驗事實之間的矛盾,有人得出了其它的量子力學的詮釋,舉例如下:
有人認為,命題演算中的“分配律”
(E∪F)∩X=E∩X+F∩X
在這裡不再適用,因此⑴式雖然成立,但從⑴式得不到⑵式,從而也得不到命題A。建立在這種看法上的量子力學詮釋稱為“非分配邏輯詮釋”,它是所謂“量子邏輯詮釋”的一種。
“哥本哈根詮釋”與“非分配邏輯詮釋”都確認全機率公式從而機率論不適用於微觀過程,前者把這一前提追溯到經典概念,而後者則把它追溯到經典邏輯。
還有一種詮釋不涉及經典概念與經典邏輯,僅僅否定機率論本身。例如,法國物理學家吉·洛查克繼承了德布羅意的觀點,認為機率論僅適用於“隱變數”,但由於某種原因,它不適用於計算測量結果的平均值。因此,洛查克確認⑴式與⑵式,但否定⑶式,從而也得不到命題A。
以建立“量子機率詮釋”著稱的L·阿卡迪提出如下論點:根據機率的頻率定義,⑴式、⑵式與⑶式適用於任何過程,但⑷式,即機率的乘法公式不適用於微觀過程,因此還是得不到命題A。阿卡迪把機率的乘法公式稱為“貝葉斯公理”,並斷言:“量子力學中的一切佯謬都是由於不適當地套用這一公理引起的。”
上面這些詮釋的存在表明:在推導命題A時,人們用了一個自以為是天經地義的前提,而它卻不適用於微觀過程。但對於究竟是哪一個前提不適用於微觀過程的問題,人們的意見不一致。
非分配邏輯詮釋、洛查克的隱變數詮釋以及阿卡迪的“量子機率詮釋”都是鮮為人知的,下面我們將認真考察這三種詮釋。
第一,試圖用“非分配邏輯”來說明量子現象也像用“三值邏輯”來說明量子現象一樣,有兩個令人沮喪的困難:第一,我們必須藉助於“布爾邏輯”來研究“非布爾邏輯”。第二,量子力學理論的數學工具是根據“布爾邏輯”展開的,如果要在“非布爾邏輯”的框架下,建立一種量子力學詮釋,那么,這種詮釋不僅要重新建立邏輯原理與物理學原理,而且還得重新建立數學原理,這是一個令人望而生畏的任務。
第二,洛查克的隱變數詮釋斷言機率論對於隱變數理論是適用的,只是不適用於被測量的“可觀察量”。但我們即將看到,微觀的事件空間是“非布爾”的,在其中某些布爾代數的規則不成立。如果在一個隱變數理論中,全部事件運算的布爾代數規則適用於隱變數,則為了使這個隱變數理論得出關於可觀察量的事件運算的規則,即使可能,也會是極為複雜而生硬的。
第三,按照的機率論教程,頻率定義的對象是“無條件機率”,而“條件機率”則通過乘法公式來定義。如果修改頻率定義使它成為“條件機率”的定義,則會立刻否定了阿卡迪的詮釋。
“修正的頻率定義”可表述如下:
定義1:考慮如下過程:某一試驗不斷重複,其中在條件S下重複了N次,而在這N次重複實驗的結果中,有NE個具有性質E。那么,當時N無限增大時,比值NE/N的極限就是在條件S下出現具有性質E的結果的機率,記作Pr(E|S)。即,
Pr(E|S)=lim[N→∞]NE/N。
而所謂“無條件機率”則具有如下意義:如果對於所考察的問題,所涉及的事件都是在一個共同的條件R條件下進行的,從而對於該問題,R是一個“先決條件”,則對於出該問題中的某一機率表達式來說,符號R 可以省去,即Pr(A|R∩B)可略寫作Pr(A|B),而Pr(A|R)就可略寫作Pr(A)。在這裡,機率表達式Pr(A)就表示“無條件機率”了。
按照這種規定,一切機率都是條件機率,所謂無條件機率只不過是略去了條件符號的條件機率。
套用定義1,不難證明
Pr(E∩F|S)=Pr(E|S)Pr(F|E∩S)。⑹
如果⑹式中的S是所考察的問題的先決條件,則該式可略寫成
Pr(E∩F)=Pr(E)Pr(F|E)。⑺
⑺式就是乘法公式,它不再是條件機率Pr(F|E)的定義,也不是一個公理,而是從頻率定義導出的一個定理了。
阿卡迪斷言⑺式不適用於微觀過程,這誠然是一種極為獨特的論點,似乎至今還沒有得到其它人的支持。但這一論點也反映一個問題:把⑺式看作一個公理或看作條件機率的定義有可能使人懷疑其普遍有效性。而當我們從機率的頻率定義導出⑺式時,這種可能性就不再存在了。
下面,我們對命題A的給出另一種推導,從另一角度排除上面三種詮釋。
在電子的雙縫衍射實驗中,分別考察如下三個過程。
第一,設電子源平穩地發射著電子,在同時打開兩條縫的條件下經歷時間T,有N個電子落在螢幕上。如果命題B成立,則過程中通過第一條縫的電子數N1與通過第二條縫的電子數N2是確定的,而且通過第一條縫落在x上的電子數n1與通過第二條縫落在x上的電子數n2也是確定的,而落在x上的電子總數則是n1+n2。設e是落在螢幕上的N個電子之一,則根據機率的頻率定義,當N足夠大時,e落在x上的機率是
Pr(X)=(n1+n2)/N;
此外,e通過第一條縫的機率和通過第二條縫的機率可分別表成
Pr(E)=N1/N,Pr(F)=N2/N。
第二,假定其它條件保持不變,僅關閉第二條縫,同樣經歷時間T,則還是會有N1個電子通過第一條縫落在螢幕上,其中還是有n1個電子落在x上。在這一過程中,已知e肯定通過第一條縫,因此它落在x上的機率為
Pr(X|E)=n1/N1。
第三,同樣,如果僅關閉第一條縫,則e落在x上的機率為
Pr(X|F)=n2/N2。
根據顯然的數字關係
(n1+n2)/N=(N1/N)*(n1/N1)+(N2/N)*(n2/N2),
我們重新得到⑸式,從而重新得到命題A。上面的推導沒有用到命題演算的分配律、機率的加法公式與乘法公式,從而排除了非分配邏輯詮釋、德布羅意或洛查克的隱變數詮釋以及阿卡迪的“量子機率詮釋”
排除了這三個詮釋,我們從命題A的推導似乎只能引出哥本哈根詮釋。但是,還有一個隱蔽的前提在這裡被忽略了。
機率假設
我們回到對命題A的第二種推導,這個推導也有一點小小的疏忽,其中有如下推理:
“設同時打開兩條縫經歷時間T,有N1個電子通過第一條縫,其中落在x上的電子數為n1。如果其它條件保持不變,僅關閉第二條縫,同樣經歷時間T,從而還是會有N1個電子通過第一條縫落在螢幕上,則其中還是會有n1個電子落在x上。”
這一推理默認了如下前提:“在雙縫衍射過程中,通過某一條縫落在x上的電子數,與另一條縫的啟閉(打開還是關閉)無關。”
為了用數學的語言表述這一命題,首先要承認“打開第二條縫”還是“關閉第二條縫”是不同是實驗條件,在這兩種實驗條件下,通過第一條縫落在x上的電子數的含義不同,必須用不同的符號來表示。用n1和m1分別表示在打開和關閉第二條縫兩種條件下通過第一條縫落在x上的電子數;用n2和m2分別表示在打開和關閉第一條縫兩種條件下通過第二條縫落在x上的電子數,則上述推理默認的前提表成:
m1=n1,m2=n2,⑻
我們把第三節所考察的三個過程中的第二、第三兩個過程合併成一個,即考慮如下兩個過程:
過程U:同時打開兩條縫經歷時間T,有N個電子落在螢幕上。
過程V:假定其它條件保持不變,先關閉第二條縫,經歷時間T,從而有N1個電子達到螢幕上;再打開第二條縫,關閉第一條縫,再經歷時間T,從而有N2個電子達到螢幕上。在整個過程中,也有N個電子落在螢幕上。
在這裡,過程U是在“兩條縫同時打開”的條件下進行的,過程V則是在“兩條縫分別輪流打開”的條件下進行的,由於兩個過程的實驗條件不同,有關的機率有不同的含義,必須用不同的符號來表示它們。如果還是用符號U和V表示這兩個過程的條件,則按照機率論的通常寫法,“在‘兩條縫同時打開’的條件下的某一事件Y的機率”本應寫成Pr(Y|U),但為了把U這一條件和其它條件區別開來,我們把這個機率表達式改寫成PrU(Y)。同樣,“在‘兩條縫分別輪流打開’的條件下的Y事件的機率”寫成PrV(Y)。如果Y事件的機率與兩條縫“同時打開”還是“分別輪流打開”無關,則仍然寫成Pr(Y)。
還是用e表示一個“落在螢幕上的電子”,E表示“e通過第一條縫”而F表示“e通過第二條縫”,X表示“e落在?上”,則根據機率的頻率定義,當N足夠大時,對於過程U,我們有:
PrU(X)=(n1+n2)/N;
PrU(X∩E)=n1/N,PrU(X∩F)=n2/N。
根據顯然的數字關係
(n1+n2)/N=n1/N+n2/N,
我們有
PrU(X)=PrU(X∩E)+PrU(X∩F)。⑼
在過程V中,落在螢幕上的電子總數還是N。還是用m1和m2分別表示通過第一條縫落在x上的電子數與通過第二條縫落在x上的電子數,則有:
PrV(X∩E)=m1/N;PrV(X∩F)=m2/N。
於是⑻式表成:
PrU(X∩E)=PrV(X∩E), PrU(X∩F)=PrV(X∩F),⑽
⑽式表示:
F:在雙縫衍射過程中,單個電子e通過某一條縫落在x上的機率,與另一條縫的啟閉無關。
⑼式和⑽式給出
PrU(X)=PrV(X∩E)+PrV(X∩F)。⑾
⑾式表示:
G:在雙縫衍射過程中,在兩條縫同時打開的條件下單個電子e落在x上的機率是在兩條縫輪流打開的條件下單個電子e落在x上的兩個機率之和。
如果說命題B表示靜電場遵循迭加原理,那么命題G就表示“機率遵循迭加原理”。但由於命題G並不是一個實驗事實,我們不能稱它為“機率的迭加原理”。儘管如此,命題G曾經給我們帶來長期的困擾,我們不得不一再提到它,因此它總得有一個名稱,下面我們稱它為“機率的迭加假設”。
考慮到x可以是螢幕上的任意區域,從命題G可以得到命題A。但是在導出命題G時,不僅用到命題B,而且還用到命題F,因此我們從雙縫衍射實驗得出的結論就不再是“命題B不成立”,而是“命題B與命題F不能同時成立”。
如果說命題B與常識是一致的,放棄它會導致“不可思議”的結論。那么,命題F卻並非如此,人們接受這個前提僅僅是由於疏忽。因此,與其放棄命題B倒不如放棄命題F。因此,我們傾向於認為命題F並不成立,即傾向於認為“機率不遵循迭加原理”。在下一節,我們將證明這一結論。
回到第三節對命題A的推導,從其中的第一個過程,我們得到的⑸式是:
PrU(X)=Pr(E)PrU(X|E)+Pr(F)PrU(X|F)。⑿
這是機率論意義下的“全機率公式”。在兩條縫同時打開的條件下,我們無法分辨一個落在x上的電子到底是通過第一條縫還是第二條縫,從而PrU(X|E)和PrU(X|F)是不能測量的。因此,⑿式根本不能與實驗結果相比較,從而也就不可能與實驗事實相矛盾。
再考慮另外兩個過程,並且把PrV理解為“另一條縫關閉”的條件下的機率符號,相應地,把PrU理解為“另一條縫打開”的條件下的機率符號,則命題G表成
PrU(X)=Pr(E)PrV(X|E)+Pr(F)PrV(X|F)。⒀
從命題B只能導出⑿式,它是機率論意義下的全機率公式,而導出命題A的則是⒀式,它是“機率迭加假設”的另一種表達式。哥本哈根學派混淆了⑿式與⒀式,這才得出“從命題B可以導出命題A”的結論。
原理
⒀式表示PrU(X)、PrV(X|E)和PrV(X|F)三個可以測量的機率之間的關係,但這一公式並不成立,為了從理論上導出這三個機率之間的關係,我們必須找到一個具有如下性質的量:
第一,滿足迭加原理;
第二,從它能計算出機率的測量值。
幸運的是,這個量已經找到,它就是“機率幅”。
費曼曾說:“機率幅”這一概念乃是量子力學的核心。實際上,“機率幅” 這一概念之所以重要,正是由於它滿足迭加原理。對於雙縫衍射實驗,這個原理可表成:“單個電子通過某一信道落在螢幕上某處的機率幅,與另一信道是否打開無關。”
機率幅是一個複數,與躍遷機率Pr(B|A)對應的機率幅記作,根據量子力學,兩者的對應關係是:
Pr(B|A)=||^2。
即Pr(B|A)是;的“模方”(絕對值的平方)。
和機率一樣,機率幅也遵循加法公式和乘法公式。
像Pr(X)這樣的“無條件機率”實際上還是有一個先決條件:“e是落在螢幕上的一個電子”。用S表示這一先決條件,則Pr(X)其實是Pr(X|S)的略寫,其對應的機率幅是;。
在雙縫衍射實驗中,兩條縫“同時打開”與“輪流打開”對於機率幅也是不同的條件。下面,我們用U和V分別表示在兩條縫同時打開和輪流打開的條件下,事件“e落在x上”的機率幅。
根據機率幅的運算規則,我們有:
U=U*+U*;。⒁
機率幅的迭加原理在這裡表成:
V=U,V=U。 ;⒂
上面兩式給出
U=V*+V*;。⒃
比較靜電場的迭加原理,這是機率幅的迭加原理在這裡的另一種表達方式。
對⒃式的兩邊取模方,再藉助於機率的測量值與機率幅之間的對應關係
PrU(X)=|U|^2,
PrV(X|E)=|V|^2,PrV(X|F)=|V|^2,
以及
Pr(E)=||^2,Pr(F)=||^2,
我們得到
PrU(X)=Pr(E)*PrV(X|E)+Pr(F)*PrV(X|F)+J。⒄
其中J是交叉項,它表現機率的干涉現象。
由於⒂式成立,⒁式和⒃式都可以略寫成
=*+*;。⒅
如果略去不言而喻的條件S,則⒅式寫成:

