理論導出
對於RCP結構,意味著用同樣尺寸的球,無規對密堆的緻密度(或填充空間的“有效”程度)大約是晶態密堆積的86%對於僅通過吸引勢相互作用的硬球(對稀有氣體固體,其原子具有封閉的殼層結構,通過分子力或范德瓦耳斯力相互作用;或對金屬,其正離子通過傳導電子相互作用,這是一個粗糙的模型),晶態密堆積相應於位能 的絕對值極小,因為這種排列給出最大的堆積密度。
對於Voronoi網路或多面體泡沫,三維歐勒-潘卡雷關係是:
V-E+F-N=1 。。。。。。。。。。。(1)
其中V是頂點數,E是邊數,F是面數, N是元胞數.
考慮把方程 (1)用到單個孤立的多面體情況,即N=1。 對於立方體:V=8,E=12,F=6.
對菱形十二面體 V=14,E=24,F=12.
對我們感興趣的統計蜂房的“平均”元胞,我們要用到已經指出的泡沫連線特性:每4個元胞(及邊)共一個 頂點,每三個元胞( 和面)共一個邊。) 因而從這個網路分割出來的單個多面體元胞每三個面(及邊)共一個頂點,每兩個面共一個邊。 加上每個多邊形面和個邊(及頂點)相接觸這一事實,所有這些拓撲信息包含在下式中
3V=2E=pF 。。。。。。。。。。。。。。。(2)
(2)帶入(1)F=12/(6-p)
 無規密堆積
無規密堆積圖1.計算機做出的100個原子的無規圖計算機作出的密堆積圖形(Barker,Hoare,Finney於1975)
RCP結構的特徵
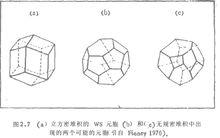
Finney對實驗建造的包含8000 個球的、無規密堆積模型進行了仔細的統計拓撲分析。特別考察了與所得 球心陣列相應的Voronoi 多面體的特點。圖2給出了兩個這類不規則的WS元胞(同時給出菱形十二面體,這是立方密排的規則元胞)。
 無規密堆積
無規密堆積圖3給出一對直方圖 ,這是按照 Finney對無規密堆積中WS元胞的拓撲統計所得到的數據畫的。對於p的分布,即不同類型的多邊型面,最常出現的是p=5 (約占總面數的41%),,然後依次是p=6(29%),p=4(19%),p=7(6%),p=3(4%) 以及p=8(1%).
對於f的分布,即每個多面體中面的數目,最常出現的是14 面元胞,然後依次為f=15,f=13,f=16,f=12 以及f=17。為比較起見注意,對具有單一元胞拓撲的晶態密堆積,分布圖在p=4和f=12處收縮為δ函式
 無規密堆積
無規密堆積