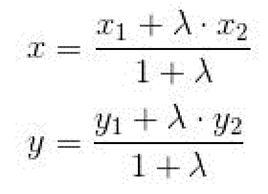基本介紹
定理1
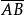 定比分點
定比分點 定比分點
定比分點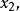 定比分點
定比分點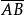 定比分點
定比分點 定比分點
定比分點設坐標軸上有向線段 的起點A和終點B的坐標分別為 和 分點M分 的比為 ,那么,分點M的坐標
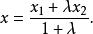 定比分點
定比分點證明: 分點M的坐標為x,那么由定理1 知
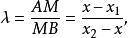 定比分點
定比分點由此得
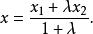 定比分點
定比分點推論
 定比分點
定比分點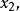 定比分點
定比分點設坐標軸上線段AB的端點A和B的坐標分別為, 和那么線段AB的中點的坐標
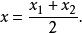 定比分點
定比分點例題解析
 定比分點
定比分點 定比分點
定比分點【 例1】 已知有兩點P(3,-2),P(-9,4),線段PP與x軸的交點P分有向線段PP所成比為 ,則有 是多少?並求P點橫坐標。
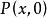 定比分點
定比分點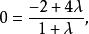 定比分點
定比分點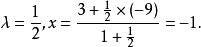 定比分點
定比分點解:設 ,則有 得
 定比分點
定比分點評註:先由起點、分點、終點的縱坐標求出 ,進一步再得到分點的橫坐標。
【 例2】 已知平行四邊形ABCD的三個頂點A(-1,-2),B(3,4),C(0,3),則頂點D的坐標為多少?
解:設平行四邊形ABCD的對角線AC,BD的交點為E(x,y),即E為AC的中點,所以
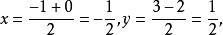 定比分點
定比分點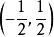 定比分點
定比分點即E點的坐標為 。
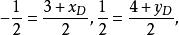 定比分點
定比分點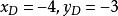 定比分點
定比分點又因為E為BD的中點,所以解得 。
評註: 利用平行四邊形性質。
【 例3】 在平面上有五個整點(坐標為整數的點),證明其中至少有兩個點的連線的中點也是整點。
證明: 設A,B,C,D,E是五個整點,則每個點的坐標的奇偶不外四種可能,就是(偶,偶)、(奇,奇)、(奇,偶)和(偶,奇)。我們取四個點A、B、C、D,它們的坐標的“最壞”情形是(偶,偶)、(奇,奇)、(奇,偶)、(偶,奇)。因為這時四個點中任意兩個點的連線的中點都不是整點,第五個點E的坐標只能是上面說的四種情形之一,但不論是哪種情形,容易驗證E與A、B、C、D中的某一點的連線的中點必是整點。
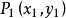 定比分點
定比分點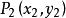 定比分點
定比分點【 例4】 在點 和 處各放置質量為m和m的質點,求證:這兩個質點組成的質點系的重心的坐標為
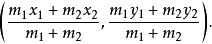 定比分點
定比分點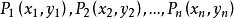 定比分點
定比分點 定比分點
定比分點在n個點 處各放置質量為 的質點,求證:這n個質點組成的質點系的重心的坐標為
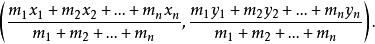 定比分點
定比分點證明:兩個質點組成的質點系的重心G線上段PP上,並且滿足條件
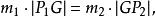 定比分點
定比分點即
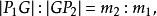 定比分點
定比分點所以
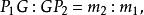 定比分點
定比分點所以重心G的坐標
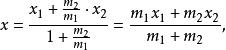 定比分點
定比分點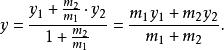 定比分點
定比分點一般情形請讀者用數學歸納法證明。
 定比分點
定比分點 定比分點
定比分點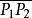 定比分點
定比分點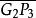 定比分點
定比分點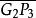 定比分點
定比分點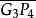 定比分點
定比分點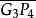 定比分點
定比分點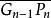 定比分點
定比分點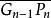 定比分點
定比分點【 例5】已知n個點 ,在有向線段 上取一點G,使G分 的比為1:1;在有向線段 上取一點G,使G分 的比為1:2;在有向線段 上取一點G使G分 的比為1:3;......;在有向線段 上取一點G,使G分 的比為1:n-1,求證:最後的分點G的坐標為
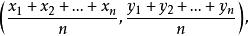 定比分點
定比分點點G叫作已知的n個點P,P,…,P的(幾何)重心(圖1)。
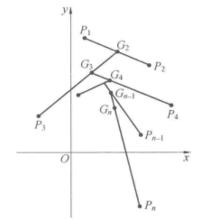 圖1
圖1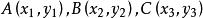 定比分點
定比分點特別地,以 為頂點的三角形的(幾何)重心的坐標為
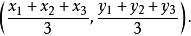 定比分點
定比分點證明: 設例4中的n個質點的質量都相等,這時n個質點的力學重心即是n個點P,P,…,P的幾何重心G,所以G的坐標為
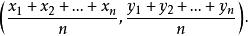 定比分點
定比分點不利用例4也可獨立證明。