基本介紹
定義1 設L是偏序集,若L的每個子集A都有上確界,下確界,即∀A⊆L,∃supA,inf A∈L,則稱L為 完備格( complete lattice);L的每一有界子集A,∃sup A,inf A∈L,則稱L是條件備格(conditionally complete Lattice)。為了方便,有時也把supA,infA表示成∨A,∧A;若∀a,b∈L,sup{a,b},inf{a,b}∈L,則稱L為格(Lattice),這時,sup{a,b}簡記為a∨b,inf{a,b}簡記為a∧b。
更一般地,還可以給出上(下)完備格,上(下)半格的概念。
如果L是偏序集,∀A⊆L,∃sup A∈L(∃ infA∈L),則稱L是 上(下)完備格;∀a,b∈L,∃a∨b∈L(∃a∧b∈L),則稱L是上(下)半格,也可記成∨(∧)半格。
例1 設X≠∅,則(P(X),⊂)構成完備格。
由定義可知,凡完備格都是格,但格不一定是完備格。
如果L是完備格,由於L的每一個元素都是∅的上界,也是∅的下界,不難看出sup ∅=0,inf ∅= 1成立。
定義2設L是完備格,L的非空子集A稱為L的完備子格,如果∀B⊆A,supB,infB∈A;設L是格,L的非空子集A稱為L的子格,如果∀a,b∈A,a∨b,a∧b∈A。
根據定義,下述事實是顯然的:0是格L的子格;格L的單元素子集{a}(a∈L)是L的子格;格L的區間[a,b](Va,b∈L,a≤b)是L的子格;格L的任意多個子格的交仍是L的子格。
在格中還可以引人零元與單位元的概念。
定義3 設L是格,如果∃0∈L,∀x∈L均有x∨0 =x成立,則稱0是L的零元;如果∃1∈L,∀x∈L均有x∧1=x成立,則稱1是L的單位元。
顯然,完備格的最小元即是零元,最大元為單位元。
命題 格L若有零元,則零元唯一;若有單位元,則單位元唯一 。
完備格的判定與基本性質
下面討論完備格的判定和一些基本性質 。
命題1 完備格定有最大元和最小元。
證明 設L是完備格,L⊆L,則∃ sup L,inf L∈L,即是L中的最大元和最小元。
為了方便,把完備格中的最大元、最小元分別記為1,0,或簡記為1,0。僅含一個元的完備格稱為 平凡的,這裡一般不考慮平凡的完備格,故當1≠0時,僅含兩個元素的完備格{0,1}就是最簡單的完備格了。
定理2 設L是偏序集
 完備格
完備格(1) 如果L中有最大元,且∀B(≠∅)⊆L,∃ infB∈L L是完備格。
 完備格
完備格(2) 如果L中有最小元,且∀B(≠∅)⊆L,∃ supB∈L L是完備格。
證明僅證(1),(2)類似可證,這裡,只須證明∃ supB∈L即可。事實上,由題設L含有最大元m,故B在L中有上界,令C是B在L中全部上界之集,則C≠∅,再由題設可知,∃infB∈L,它既是B在L中的上界,又是B在L中的最小上界,即∃ supB∈L。
定理3(1)有限格L是完備格。
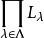 完備格
完備格(2)一族完備格{L|λ∈Λ}的直積L= 是完備格。
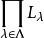 完備格
完備格推論4 一族格{L|λ∈Λ}的直積 是格 。

