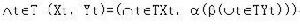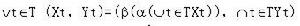概念格

假設給定形式背景(con 表1給出一個形式背景，其對應的概念格如圖1所示。 在經典定義中，形式背景是二值的。

概念格（Concept Lattices）定義：
假設給定形式背景(context)為三元組T=(O，D，R)，其中O是事例集合，D是描述符（屬性）集合，R是O和D之間的一個二元關係，則存在唯一的一個偏序集合與之對應，並且這個偏序集合產生一種格結構，這種由背景(O，D，R)所誘導的格L就稱為一個概念格。格L中的每個節點是一個序偶（稱為概念），記為(X，Y)，其中XÎP(O)稱為概念的外延；YÎP(D)稱為概念的內涵。每一個序偶關於關係R是完備的，即有性質：

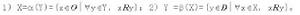
在概念格節點間能夠建立起一種偏序關係。給定H1=( X1，Y1) 和 H2=( X2，Y2)，則H1< H2 &Ucirc; Y1&Igrave; Y2，領先次序意味著H1是H2的父節點或稱直接泛化。根據偏序關係可生成格的Hasse圖：如果H1<H2並且不存在另一個元素H3使得H1<H3<H2，則從H1到H2就存在一條邊。

表1給出一個形式背景，其對應的概念格如圖1所示。
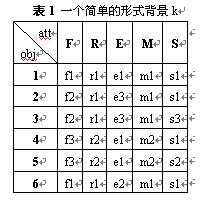
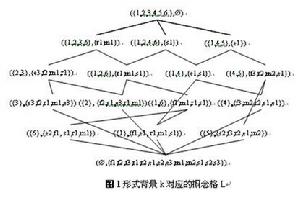
概念格的基本定理表明上述方式定義的概念和偏序關係是一個完全格。其中任意一組概念的上下確界是:

上述定義實際上對原始概念格的定義有所擴充。在經典定義中，形式背景是二值的。即每個屬性的值為1時代表該屬性在該對象中出現，為0時代表不出現。上述定義將其擴展的多值形式背景。實際上它們是等價的，很容易將多值形式背景轉變成二值形式背景。值得注意的是，多值形式背景中的屬性-值對對應於二值形式背景中的屬性。對於多值的形式背景，也可以通過概念縮放(concept scaling)來將其轉換成二值的形式背景（房明民）。