簡介
在數學，特別是點集拓撲學中，拓撲空間的子集S的完備集是S的所有極限點的集合。它通常記為S'。
這個概念是格奧爾格·康托爾在1872年介入的，他開發集合論很大程度上就是為了研究在實直線上的導出集合。
完備集公理
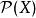完備集
完備集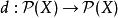完備集是拓撲學的基礎概念之一，可以用來定義拓撲空間。 給定集合X，考慮一個定義在X的冪集上的運算 ，若d滿足以下完備集 公理，則稱d為完備集 運算：
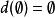完備集D：
完備集D：
完備集D：
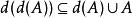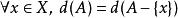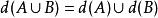完備集D：
d(A)稱為A的完備集 。
相關概念
聚點
d(A)中的點稱為A的聚點。
性質
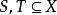完備集
完備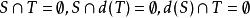集
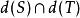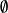完備集
完備集，若 。則稱S和T是分離的。（注意： 不一定為 ）。
集合S被定義為 完美的，如果S=d(S)。等價地說，完美集合是沒有孤點的閉集。完美集合又稱為完備集合。
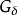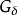完備集 完備集Cantor-Bendixson定理聲稱任何波蘭空間都可以寫為可數集合和完美集合的的並集。因為任何波蘭空間的 子集都再次是波蘭空間，這個定理還證明了任何波蘭空間的 子集都是可數集合和完美集合的並集。
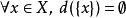完備集拓撲空間X是T空間，若且唯若 。
參見
•極限點
•導出代數
