概念
 學生化殘差
學生化殘差 學生化殘差
學生化殘差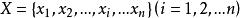 學生化殘差
學生化殘差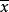 學生化殘差
學生化殘差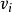 學生化殘差
學生化殘差設對某量進行 次獨立測量,得到的測量列 為 ,它的算數平方值 及其殘差 分別為:
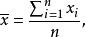 學生化殘差
學生化殘差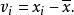 學生化殘差
學生化殘差定義殘差與實驗標準差之比為 實驗學生化殘差,即:
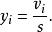 學生化殘差
學生化殘差 學生化殘差
學生化殘差式中, 為標準差,其值為:
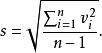 學生化殘差
學生化殘差殘差與樣本標準差之比為 樣本學生化殘差計算方法不變。在一般情況下,實驗學生化殘差和樣本學生化殘差均可簡稱為 學生化殘差。
殘差的絕對值與標準差之比為實驗學生化殘差的絕對值,即:
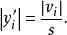 學生化殘差
學生化殘差一般情況下,學生化殘差的絕對值可以分為實驗學生化殘差的絕對值和樣本學生化殘差的絕對值。
性質
性質1
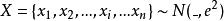 學生化殘差
學生化殘差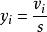 學生化殘差
學生化殘差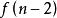 學生化殘差
學生化殘差若 ,則 服從湯姆森 分布.
性質2
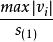 學生化殘差
學生化殘差若某一測量列的樣本學生化殘差之絕對值的最大值為 ,那么多個測量列的樣本學生化殘差之絕對值的最大值分別滿足:
 學生化殘差
學生化殘差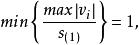 學生化殘差
學生化殘差當 為偶數時,
 學生化殘差
學生化殘差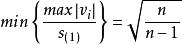 學生化殘差
學生化殘差當 為奇數時, 。
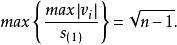 學生化殘差
學生化殘差性質3
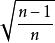 學生化殘差
學生化殘差將性質2中公式兩端分別乘以 ,可得:
 學生化殘差
學生化殘差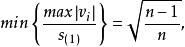 學生化殘差
學生化殘差當 為偶數時,
 學生化殘差
學生化殘差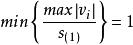 學生化殘差
學生化殘差當 為奇數時, 。
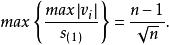 學生化殘差
學生化殘差套用
1.殘差分析中的套用
 學生化殘差
學生化殘差 學生化殘差
學生化殘差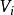 學生化殘差
學生化殘差 學生化殘差
學生化殘差 學生化殘差
學生化殘差在測量上 ,殘差圖就是以學生化殘差 為縱坐標 ,觀測值的中心化值 為橫坐標的散點圖。當有邊 、角觀測量時 ,可分別繪製殘差圖。由於殘差 ,作為誤差 的觀測值或 “估計 應該與 相差不遠 ,因此 ,根據殘差圖的大致形狀是否與應有的性質相一致 ,就可以對假設的合理性提供一些有益的信息。
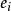 學生化殘差
學生化殘差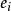 學生化殘差
學生化殘差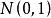 學生化殘差
學生化殘差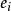 學生化殘差
學生化殘差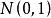 學生化殘差
學生化殘差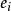 學生化殘差
學生化殘差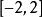 學生化殘差
學生化殘差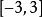 學生化殘差
學生化殘差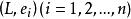 學生化殘差
學生化殘差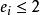 學生化殘差
學生化殘差由於學生化殘差 近似服從 ,且近似相互獨立 ,因此 ,這些可看作來自母體的簡單 隨機樣本。根據標準常態分配的性質 ,大約應有95%的 落在 中,更進一 步約有97%的落在 中。又因學生化殘差相關性很小 ,所以,在殘差圖中點 應大致落在 的水平帶內 ,且不呈現任何趨勢。
當發現殘差圖有異常現象 ,可對症下藥 ,通過剔除異常觀測值 ,或改變權陣等方法進行處理 ,直到殘差圖無異常現象為止。
2.數據診斷中的套用
1.強影響點
強影響點就是對統計推斷有很大影響的觀測數據。到目前為止 ,已經有很多方法 度量一個觀測數據對參數估計的影響 ,其中主要的一類是以 Cook 距離作為度量 影響標準的經驗影響函式。在測量上一般定義為:
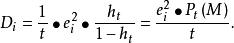 學生化殘差
學生化殘差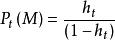 學生化殘差
學生化殘差 學生化殘差
學生化殘差 學生化殘差
學生化殘差其中, 是 的單調遞增函式。套用上常把 所對應的觀測值稱為強影響點。強影響點對參數估值的影響類似於強權點 ,但二者又有區別。強影響點除了同強權點一樣反映了觀測值在控制網結構中的位置外 ,還包含了學生化殘差的影響。
2.異常分析
一個觀測值 ,如果它的學生化殘差 比其它觀測值的學生化殘差大得多 ,就稱此觀測值為異常點。也就是可 能含有粗差的觀測值 它有可能對平差結果產生非同小可的影響。因此。如何 進行粗差檢測是近幾年倍受重視的問題。粗差作為模型誤差 ,既可把它歸入函式模型用識別法檢測 ,又可把它歸入隨機模型用調節法處理。
