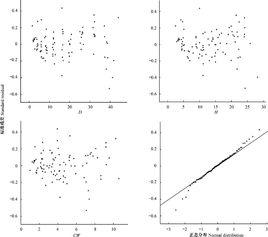
普通殘差
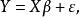 殘差
殘差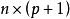 殘差
殘差設線性回歸模型為 其中 Y是由回響變數構成的n維向量,X是 階設計矩陣, β是p+1維向量, ε是n維隨機變數。
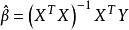 殘差
殘差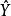 殘差
殘差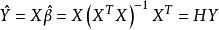 殘差
殘差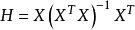 殘差
殘差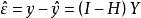 殘差
殘差回歸係數的估計值,擬合值 為,其中,稱H為帽子矩陣。殘差為。
這解釋了帽子矩陣與殘差的關係,因為殘差可以通過帽子矩陣與真實值得出。
內學生化殘差
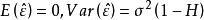 殘差
殘差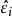 殘差
殘差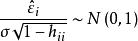 殘差
殘差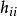 殘差
殘差由差向量 ε的的性質,得到。因此,對每個,有,其中是矩陣H對角線上的元素。
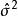 殘差
殘差 殘差
殘差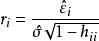 殘差
殘差 殘差
殘差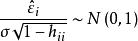 殘差
殘差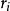 殘差
殘差用作為的估計值,稱為標準化殘差,或者稱為內學生化殘差。這因為的估計中用了包括第i個樣本在內的全部數據。由可知,標準化殘差近似服從標準常態分配。
外學生化殘差
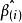 殘差
殘差 殘差
殘差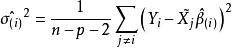 殘差
殘差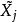 殘差
殘差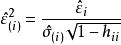 殘差
殘差若記刪除第i個樣本數據後,由余下的n-1個樣本數據求得的回歸係數為,做的估計值,有,其中為設計矩陣X的第j行。稱為學生化殘差,或者稱為外學生化殘差。
特徵
在回歸分析中,測定值與按回歸方程預測的值之差,以δ表示。殘差δ遵從常態分配N(0,σ2)。(δ-殘差的均值)/殘差的標準差,稱為標準化殘差,以δ*表示。δ*遵從標準常態分配N(0,1)。實驗點的標準化殘差落在(-2,2)區間以外的機率≤0.05。若某一實驗點的標準化殘差落在(-2,2)區間以外,可在95%置信度將其判為異常實驗點,不參與回歸直線擬合。
顯然,有多少對數據,就有多少個殘差。殘差分析就是通過殘差所提供的信息,分析出數據的可靠性、周期性或其它干擾。
分析
為了更深入地研究某一自變數與因變數的關係,人們還引進了偏殘差。此外, 還有學生化殘差、預測殘差等。以某種殘差為縱坐標,其它變數為橫坐標作散點圖,即殘差圖 ,它是殘差分析的重要方法之一。通常橫坐標的選擇有三種:
(1) 因變數的擬合值;
(2)自變數;
(3)當因變數的觀測值為一時間序列時,橫坐標可取觀測時間或觀測序號。
殘差圖的分布趨勢可以幫助判明所擬合的線性模型是否滿足有關假設。如殘差是否近似常態分配、是否方差齊次,變數間是否有其它非線性關係及是否還有重要自變數未進入模型等。.當判明有某種假設條件欠缺時, 進一步的問題就是加以校正或補救。需分析具體情況,探索合適的校正方案,如非線性處理,引入新自變數,或考察誤差是否有自相關性。