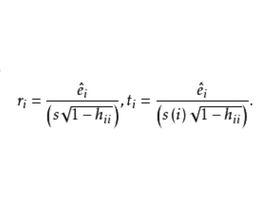基本介紹
學生化內殘差
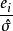學生化外殘差
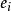學生化外殘差
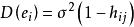學生化外殘差
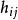學生化外殘差
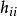學生化外殘差
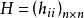學生化外殘差線上性回歸中，殘差的重要套用之一是根據它的絕對值大小判定異常點，通常採用標準化殘差。但由於普通殘差的方差為，所以標準化殘差雖然除去了因變數的度量單位的影響，但沒有除去的影響，這裡是帽子矩陣的對角線元素。為此，令
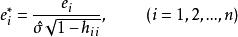學生化外殘差稱為 學生化(內)殘差。它比用標準殘差判斷異常點，更適用 。
學生化外殘差
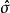學生化外殘差
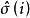學生化外殘差學生化外殘差也叫學生化刪除的殘差，把學生化殘差中的用代替，即
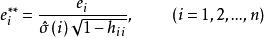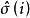學生化外殘差 學生化外殘差
學生化外殘差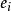 學生化外殘差 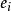學生化外殘差稱作 學生化刪除的殘差，其中表示刪除了第i次觀察值所剩的n-1次觀察進行回歸擬合後所算出的標準誤差的估計值。其用意是，在對普通殘差作“標準化”時，排除自身在誤差方差中的份額。
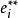學生化外殘差
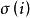學生化外殘差在計算時，不必對每個i做一次回歸來計算，可由以下公式直接計算：
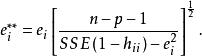學生化外殘差公式中所有數據都是根據n個觀察值的擬合回歸模型得來的 。
相關介紹與性質
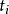學生化外殘差
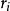學生化外殘差學生化殘差有兩種：和，它們都是重要的診斷統計量，除了學生化殘差外，自從20世紀70年代以來，人們出於各種目的，提出了許多類的殘差以及相應的診斷統汁量，比較常見的有三種殘差，分別是預測殘差、不相關殘差和遞推殘差 。
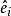學生化外殘差 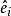學生化外殘差 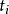學生化外殘差 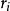學生化外殘差 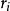學生化外殘差 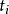學生化外殘差在實際套用中，普通殘差並不直接被套用，主要是各個不存在同方差性，不便於比較，這就要求對進行標準化處理後得到學生化殘差。學生化殘差有兩種：和，它們都是重要的診斷統計量，模型(3．1)式的學生化內殘差(internal studentized residuals)和學生化外殘差(external studentized residuals)定義為：
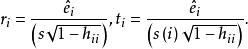學生化外殘差 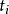學生化外殘差 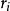學生化外殘差這兩個統計量在異常點檢驗中都非常重要，學生化外殘差就是異常點檢驗的t統計量，由學生化內殘差可得到異常點檢驗的似然比統計量。
對於學生化殘差有以下性質成立。
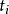學生化外殘差
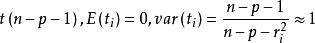學生化外殘差(t)服從；
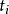學生化外殘差 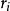學生化外殘差
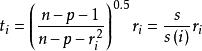學生化外殘差(2)為的單調遞增函式，；
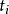學生化外殘差
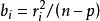學生化外殘差
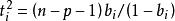學生化外殘差(3)為單調遞增函式，；
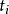學生化外殘差
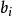學生化外殘差
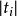學生化外殘差 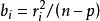學生化外殘差和可看作殘差分析的定量結果，當或超過一定水平，則可認為第i個樣本是異常點 。
