簡介
對線性回歸模型
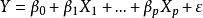 多重共線性
多重共線性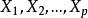 多重共線性
多重共線性基本假設之一是自變數, 之間不存在嚴格的線性關係。如不然,則會對回歸參數估計帶來嚴重影響。為了說明這一點,首先來計算線性回歸模型參數的 LS 估計的均方誤差。為此。重寫線性回歸模型的矩陣形式為
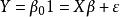 多重共線性
多重共線性 多重共線性
多重共線性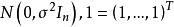 多重共線性
多重共線性 多重共線性
多重共線性 多重共線性
多重共線性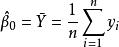 多重共線性
多重共線性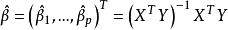 多重共線性
多重共線性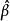 多重共線性
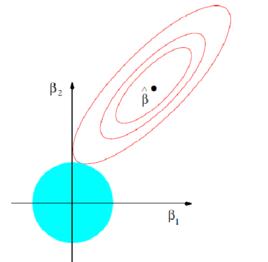
多重共線性其中 服從多元常態分配,設計矩陣 X 是 的,且秩為 p。這時,參數 的 LS 估計為,而回歸係數的 LS 估計為。注意到由此獲得的 LS 估計是無偏的,於是估計 的均方誤差為
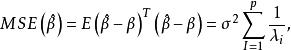 多重共線性
多重共線性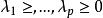 多重共線性
多重共線性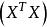 多重共線性
多重共線性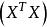 多重共線性
多重共線性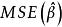 多重共線性
多重共線性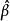 多重共線性
多重共線性 多重共線性
多重共線性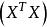 多重共線性
多重共線性其中 是 的特徵根。顯然,如果至少有一個特徵根非常接近於零,則 就很大,也就不再是 的一個好的估計。由線性代數的理論知道,若矩陣的某個特質根接近零,就意味著矩陣 X 的列向量之間存在近似線性關係。
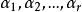 多重共線性
多重共線性如果存在一組不全為零的數,使得
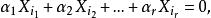 多重共線性
多重共線性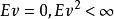 多重共線性
多重共線性則稱線性回歸模型存在完全共線性;如果還存在隨機誤差 v,滿足,使得
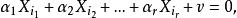 多重共線性
多重共線性則稱線性回歸模型存在非完全共線性。
如果線性回歸模型存在完全共線性,則回歸係數的 LS 估計不存在,因此,線上性回歸分析中所談的共線性主要是非完全共線性,也稱為復共線性。判斷復共線性及其嚴重程度的方法主要有特徵分析法(analysis of eigenvalue),條件數法 (conditional numbers)和方差擴大因子法(variance inflation factor)。
產生原因
主要有3個方面:
(1)經濟變數相關的共同趨勢
(2)滯後變數的引入
(3)樣本資料的限制
影響
(1)完全共線性下參數估計量不存在
(2)近似共線性下OLS估計量非有效
多重共線性使參數估計值的方差增大,1/(1-r2)為方差膨脹因子(Variance Inflation Factor, VIF)如果方差膨脹因子值越大,說明共線性越強。相反 因為,容許度是方差膨脹因子的倒數,所以,容許度越小,共線性越強。可以這樣記憶:容許度代表容許,也就是許可,如果,值越小,代表在數值上越不容許,就是越小,越不要。而共線性是一個負面指標,在分析中都是不希望它出現,將共線性和容許度聯繫在一起,容許度越小,越不要,實際情況越不好,共線性這個“壞蛋”越強。進一步,方差膨脹因子因為是容許度倒數,所以反過來。
總之就是找容易記憶的方法。
(3)參數估計量經濟含義不合理
(4)變數的顯著性檢驗失去意義,可能將重要的解釋變數排除在模型之外
(5)模型的預測功能失效。變大的方差容易使區間預測的“區間”變大,使預測失去意義。
需要注意:即使出現較高程度的多重共線性,OLS估計量仍具有線性性等良好的統計性質。但是OLS法在統計推斷上無法給出真正有用的信息。
判斷方法
 多重共線性
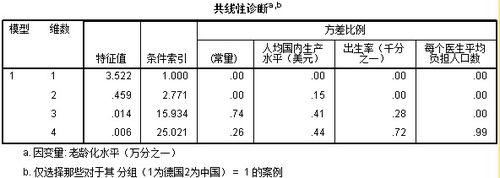
多重共線性如圖,是對德國人口老齡化情況的分析,其中y是老齡化情況,線性回歸的x1、x2、x3分別為人均國內生產總值、出生率、每個醫生平均負擔人口數。
判斷方法1:特徵值,存在維度為3和4的值約等於0,說明存在比較嚴重的共線性。
判斷方法2:條件索引列第3第4的值大於10,可以說明存在比較嚴重的共線性。
判斷方法3:比例方差記憶體在接近1的數(0.99),可以說明存在較嚴重的共線性。
解決方法
(1)排除引起共線性的變數
找出引起多重共線性的解釋變數,將它排除出去,以逐步回歸法得到最廣泛的套用。
(2)差分法
時間序列數據、線性模型:將原模型變換為差分模型。
(3)減小參數估計量的方差:嶺回歸法(Ridge Regression)。