簡介
多元統計分析
multivariate statistical analysis
研究客觀事物中多個變數(或多個因素)之間相互依賴的統計規律性。它的重要基礎之一是多元正態分析。又稱多元分析 。 如果每個個體有多個觀測數據,或者從數學上說, 如果個體的觀測數據能表為 P維歐幾里得空間的點,那么這樣的數據叫做多元數據,而分析多元數據的統計方法就叫做多元統計分析 。 它是數理統計學中的一個重要的分支學科。20世紀30年代,R.A.費希爾,H.霍特林,許寶碌以及S.N.羅伊等人作出了一系列奠基性的工作,使多元統計分析在理論上得到迅速發展。50年代中期,隨著電子計算機的發展和普及 ,多元統計分析在地質 、氣象、生物、醫學、圖像處理、經濟分析等許多領域得到了廣泛的套用 ,同時也促進了理論的發展。各種統計軟體包如SAS,SPSS等,使實際工作者利用多元統計分析方法解決實際問題更簡單方便。重要的多元統計分析方法有:多重回歸分析(簡稱回歸分析)、判別分析、聚類分析、主成分分析、對應分析、因子分析、典型相關分析、多元方差分析等。
早在19世紀就出現了處理二維正態總體(見常態分配)的一些方法,但系統地處理多維機率分布總體的統計分析問題,則開始於20世紀。人們常把1928年維夏特分布的導出作為多元分析成為一個獨立學科的標誌。20世紀30年代,R.A.費希爾、H.霍特林、許寶?以及S.N.羅伊等人作出了一系列奠基性的工作,使多元統計分析在理論上得到了迅速的進展。40年代,多元分析在心理、教育、生物等方面獲得了一些套用。由於套用時常需要大量的計算,加上第二次世界大戰的影響,使其發展停滯了相當長的時間。50年代中期,隨著電子計算機的發展和普及,它在地質、氣象、標準化、生物、圖像處理、經濟分析等許多領域得到了廣泛的套用,也促進了理論的發展。
多元分析發展的初期,主要討論如何把一元正態總體的統計理論和方法推廣到多元正態總體。多元正態總體的分布由兩組參數,即均值向量μ(見數學期望)和協方差矩陣(簡稱協差陣)∑ (見矩)所決定,記為Np(μ,∑)(p為分布的維數,故又稱p維常態分配或p 維正態總體)。設X1,X2,…,Xn為來自正態總體Np(μ,∑)的樣本,則μ和∑的無偏估計(見點估計)分別是
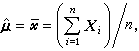 公式
公式和
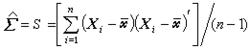 公式
公式分別稱之為樣本均值向量和樣本協差陣,它們是在各種多元分析問題中常用的統計量。樣本相關陣R 也是一個重要的統計量,它的元素為
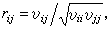 公式
公式其中υij為樣本協差陣S的元素。S的分布是維夏特分布,它是一元統計中的Ⅹ2分布的推廣。
另一典型問題是:假定兩個多維常態分配協差陣相同,檢驗其均值向量是否相同。設樣本X1,X2,…,Xn抽自正態總體Np(μ1,∑),而Y1,Y2,…,Ym抽自Np(μ2,∑),要檢驗假設H 0:μ1=μ2(見假設檢驗)。在一元統計中使用t統計量(見統計量)作檢驗;在多元分析中則用T2統計量,
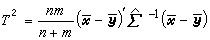 公式
公式,其中,
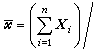 公式
公式,
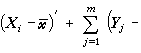 公式
公式·
,T2的分布稱為T2分布。這是H.霍特林在1936年提出來的。
在上述問題中的多元與一元相應的統計量是類似的,但並非都是如此。例如,要檢驗k個正態總體的均值是否相等,在一元統計中是導致F統計量,但在多元分析中可導出許多統計量,最著名的有威爾克斯Λ統計量和最大相對特徵根統計量。研究這些統計量的精確分布和優良性是近幾十年來多元統計分析的重要理論課題。
多元統計分析有狹義與廣義之分,當假定總體分布是多元常態分配時,稱為狹義的,否則稱為廣義的。近年來,狹義多元分析的許多內容已被推廣到更廣的分布之中,特別是推廣到一種稱為橢球等高分布族之中。
按多元分析所處理的實際問題的性質分類,重要的有如下幾種。
多重回歸分析
簡稱回歸分析。其特點是同時處理多個因變數。回歸係數和常數的計算公式與通常的情況相仿,只是由於因變數不止一個,原來的每個回歸係數在此都成為一個向量。因此,關於回歸係數的檢驗要用T2統計量;對回歸方程的顯著性檢驗要用Λ統計量。
回歸分析在地質勘探的套用中發展了一種特殊的形式,稱為趨勢面分析,它以各種元素的含量作為因變數,把它們對地理坐標進行回歸(選用一次、二次或高次的多項式),回歸方程稱為趨勢面,反映了含量的趨勢。殘差分析是趨勢面分析的重點,找出正的殘差異常大的點,在這些點附近,元素的含量特別高,這就有可能形成可采的礦位。這一方法在其他領域也有套用。
判別分析
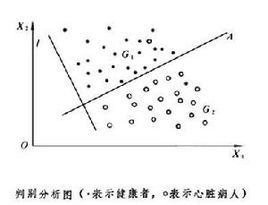
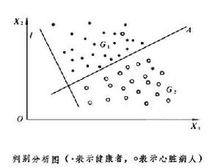 判別分析圖
判別分析圖由 k個不同總體的樣本來構造判別函式,利用它來決定新的未知類別的樣品屬於哪一類,這是判別分析所處理的問題。它在醫療診斷、天氣預報、圖像識別等方面有廣泛的套用。例如,為了判斷某人是否有心臟病,從健康的人和有心臟病的人這兩個總體中分別抽取樣本,對每人各測兩個指標X1和X2,點繪如圖 。
可用直線A將平面分成g1和g2兩部分,落在g1的絕大部分為健康者,落在g2的絕大部分為心臟病人,利用A的垂線方向l=(l1,l2)來建立判別函式
y=l1X1+l2X2,可以求得一常數с,使 y<с 等價於(X1,X2)落在g1,y>с等價於(X1,X2)落在g2。由此得判別規則:若,l1X1+l2X2
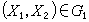 .
.判,
即此人為健康者;若,l1X1+l2X2>C
判,
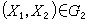 .
.即此人為心臟病人;若,l1X1+l2X2=c則為待判。此例的判別函式是線性函式,它簡單方便,在實際問題中經常使用。但有時也用非線性判別函式,特別是二次判別函式。建立判別函式和判別規則有不少準則和方法,常用的有貝葉斯準則、費希爾準則、距離判別、回歸方法和非參數方法等。
無論用哪一種準則或方法所建立的判別函式和判別規則,都可能產生錯判,錯判所占的比率用錯判機率來度量。當總體間區別明顯時,錯判機率較小;否則錯判機率較大。判別函式的選擇直接影響到錯判機率,故錯判機率可用來比較不同方法的優劣。
變數(如上例中的X1和X2)選擇的好壞是使用判別分析的最重要的問題,常用逐步判別的方法來篩選出一些確有判別作用的變數。利用序貫分析的思想又產生了序貫判別分析。例如醫生在診斷時,先確定是否有病,然後確定是哪個系統有病,再確定是什麼性質的病等等。
聚類分析
又稱數值分類。聚類分析和判別分析的區別在於,判別分析是已知有多少類和樣本來自哪一類,需要判別新抽取的樣本是來自哪一類;而聚類分析則既不知有幾類,也不知樣本中每一個來自哪一類。例如,為了制定服裝標準,對 N個成年人,測量每人的身高(x1)、胸圍(x2)、肩寬(x3)、上體長(x4)、手臂長(x5)、前胸(x6)、後背(x7)、腰圍(x8)、臀圍(x9)、下體長(x10)等部位,要將這N個人進行分類,每一類代表一個號型;為了使用和裁剪的方便,還要對這些變數(x1,x2,…,x10)進行分類。聚類分析就是解決上述兩種分類問題。
設已知N個觀測值X1,X2,…,Xn,每個觀測值是一個p維向量(如上例中人的身高、胸圍等)。聚類分析的思想是將每個觀測值Xi看成p維空間的一個點,在p維空間中引入“距離”的概念,則可按各點間距離的遠近將各點(觀測值)歸類。若要對 p個變數(即指標)進行分類,常定義一種“相似係數”來衡量變數之間的親密程度,按各變數之間相似係數的大小可將變數進行分類。根據實際問題的需要和變數的類型,對距離和相似係數有不同的定義方法。
按距離或相似係數分類,有下列方法。①凝聚法:它是先將每個觀察值{Xi}看成一類,逐步歸併,直至全部觀測值並成一類為止,然後將上述並類過程畫成一聚類圖(或稱譜系圖),利用這個圖可方便地得到分類。②分解法:它是先將全部觀測值看成一類,然後逐步將它們分解為2類、3類、…、N類,它是凝聚法的逆過程。③動態聚類法:它是將觀測值先粗糙地分類,然後按適當的目標函式和規定的程式逐步調整,直至不能再調為止。
若觀察值X1,X2,…,Xn之間的次序在分類時不允許打亂,則稱為有序分類。例如在地質學中將地層進行分類,只能將互相鄰接的地層分成一類,不能打亂上下的次序。用於這一類問題中的重要方法是費希爾於1958年提出的最優分割法。
聚類分析也能用於預報洪水、暴雨、地震等災害性問題,其效果比其他統計方法好。但它在理論上還很薄弱,因為它不象其他方法那樣有確切的數學模型。
主成分分析
又稱主分量分析,是將多個變數通過線性變換以選出較少個數重要變數的一種方法。設原來有p個變數x1,x2,…,xp,為了簡化問題,選一個新變數z,
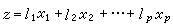 公式
公式,
要求z儘可能多地反映p個變數的信息,以此來選擇l1,l2,…,lp,當l1,l2,…,lp選定後,稱z為x1,x2,…,xp的主成分(或主分量)。有時僅一個主成分不足以代表原來的p個變數,可用q(
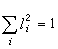 公式
公式的約束下,選擇l1,l2,…,lp使z的方差達到最大。
在根據樣本進行主成分分析時又可分為R型分析與Q型分析。前者是用樣本協差陣(或相關陣)的特徵向量作為線性函式的係數來求主成分;後者是由樣品之間的內積組成的內積陣來進行類似的處理,其目的是尋找出有代表性的“典型”樣品,這種方法在地質結構的分析中常使用。
對應分析
這是70年代地質學家提出的方法。對非負值指標的樣本資料矩陣作適當的處理後,同時進行R型與Q型的主成分分析,將結果綜合在圖上進行解釋,可以得到指標隨時間、空間位置變化的規律。它的理論正在引起多方面的重視。
因子分析
它是由樣本的資料將一組變數
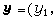 公式
公式y2,……yp)
分解為一些公共因子f與特殊因子s的線性組合,即有常數矩陣A使у=Af+s。公共因子f 的客觀內容有時是明確的,如在心理研究中,根據學生的測驗成績(指標)來分析他的反應快慢、理解深淺(公共因子);有時則是不明確的。為了尋求易於解釋的公共因子,往往對因子軸進行鏇轉,鏇轉的方法有正交鏇轉,斜鏇轉,極大變差鏇轉等。
從樣本協差陣或相關陣求公共因子的方法有廣義最小二乘法、最大似然法與不加權的最小二乘法等。通常在套用中,最方便的是直接利用主成分分析所得的頭幾個主成分,它們往往是對各個指標影響都比較大的公共因子。
典型相關分析
它是尋求兩組變數各自的線性函式中相關係數達到最大值的一對,這稱為第一對典型變數,還可以求第二對,第三對,等等,這些成對的變數,彼此是不相關的。各對的相關係數稱為典型相關係數。通過這些典型變數所代表的實際含意,可以找到這兩組變數間的一些內在聯繫。典型相關分析雖然30年代已經出現,但至今未能廣泛套用。
上述的各種方法可以看成廣義多元分析的內容,在有些方法中,如加上正態性的假定,就可以討論一些更深入的問題,例如線性模型中有關線性假設檢驗的問題,在正態的假定下,就有比較系統的結果。 多元分析也可按指標是離散的還是連續的來區分,離散值的多元分析實質上與列聯表分析有很大部分是類似的,甚至是一樣的。
非數量指標數量化的理論和方法也是廣義多元分析的一個重要的研究課題。
圖書2信息
書 名: 多元統計分析
作者:張潤楚
出版社: 科學出版社
出版時間: 2010年8月2日
ISBN: 9787030177797
開本: 16開
定價: 46.00元
內容簡介
本書講述多元統計的基礎理論和多元數據的分析方法。
作者簡介
張潤楚,南開大學數學科學學院教授,博士生導師,1966年畢業於南開大學數學系並留校任教至今,長期擔任機率信息統計教研室副任、統計學系主任、學校數學學科語言組委員等職。現兼任教育部數學與統計學教學指導委員會委員、天津市統計學副會長、中國現場統計研究會常務理事、中國統計學會理事等職。多元統計,數據分析,統計理論推斷以及機率統計在保險精算中的套用等。先後主持承擔國家自然科學基金項目5項,教育部博士點學科基金項目1項,天津市科學基金項目1項,現正在主持承擔國家自然科學基金項目“試驗設計若干最新問題研究”。先後在“套用數學學報”和“科學通報”等國內外學術刊物發表論文50多篇。
圖書目錄
《大學數學科學叢書》序
前言
符號表
第一章 隨機向量和多元常態分配
§1.1 隨機向量及有關概念
§1.2 多元常態分配
§1.3 正態向量的條件分布和相關性
§1.4 正態隨機陣的若干性質
§1.5 橢球等高分布族
§1.6 指數型分布族
§1.7 其他一些多元分布
習題一
第二章 Wishart分布, T2分布, 多元Beta和Λ分布
§2.1 正態向量的二次型
§2.2 Wishart分布及其性質
§2.3 Hotelling T2分布
§2.4 多元Beta分布及有關統計量
§2.5 附註
習題二
第三章 多元分布的參數估計
§3.1 常態分配均值向量和協差陣的估計
§3.2 常態分配廣義方差和相關係數的極大似然估計
§3.3 多元分布參數估計的某些一般理論
§3.4 附註
習題三
第四章 統計假設檢驗
§4.1 一般假設檢驗問題和似然比檢驗統計量
§4.2 協方差陣已知時正態總體均值向量的檢驗
§4.3 協方差陣Σ未知時正態總體均值向量的檢驗
§4.4 正態總體均值向量受約束情形的檢驗
§4.5 一般總體均值的大樣本推斷
§4.6 正態總體協方差陣的檢驗
§4.7 多個正態總體的參數檢驗問題
§4.8 其他基本檢驗策略原則
習題四
第五章 多元線性統計模型
§5.1 引言和基本模型
§5.2 正態回歸模型的參數MLE估計及預測
§5.3 線性回歸模型參數的最小二乘估計及其性質
§5.4 廣義線性回歸模型的參數估計及其性質
§5.5 正態回歸模型參數的假設檢驗
§5.6 設計陣X降秩情形的回歸
§5.7 多元方差分析
§5.8 回歸變數的選擇
習題五
第六章 判別分析
§6.1 距離判別
§6.2 Bayes判別
§6.3 Fisher判別法
習題六
第七章 主成分分析
§7.1 引言
§7.2 數據擬合思想
§7.3 主成分分析的套用
§7.4 對多元總體的主成分分析及其估計與檢驗
習題七
第八章 因子分析
§8.1 引言
§8.2 基本因子分析模型
§8.3 因子模型的基本性質
§8.4 因子模型的求解
§8.5 因子得分
§8.6 方差最大正交鏇轉
§8.7 總體因子分析模型及其參數估計和假設檢驗
習題八
第九章 相應分析
§9.1 引言
§9.2 相應分析的一般提法
§9.3 相應分析的求解
§9.4 相應分析的適用性檢驗
習題九
第十章 聚類分析
§10.1 相似和距離
§10.2 系統聚類法
§10.3 一次形成聚類法
§10.4 K水準逐步形成聚類法
§10.5 有序樣品的聚類方法
§10.6 移動中心聚類法
習題十
第十一章 典型相關分析
§11.1 問題的闡述和記號
§11.2 求解方法和典型變數的性質
§11.3 典型分析的幾何解釋
§11.4 典型得分和預測
§11.5 定性數據的典型分析
習題十一
第十二章 多維標度法
§12.1 引言
§12.2 距離陣和經典解
§12.3 經典解的優良性質
§12.4 非度量方法
習題十二
參考文獻
附錄A 代數補充知識
§A.1 矩陣運算
§A.2 分塊求逆和廣義逆
§A.3 幾種特殊矩陣及其性質
§A.4 矩陣微分及變換Jacobi行列式
習題A
附錄B 幾種常用分布表
表B.1 常態分配上尾機率
表B.2 t分布上側分位點tα(n)
表B.3 χ2分布上側分位點χ2α(ν)
表B.4 F分布上側分位點Fα(ν1, ν2)
表B.5 WilksΛ分布上側分位點Λα(p, n, m)
名詞索引
* * *
《大學數學科學叢書》已出版書目
多元統計分析
作者:符想先,靳劉蕊,王兢 著
出 版 社:鄭州大學出版社
出版時間:2009-12-1
版次:1
頁數:316
字數:365000
印刷時間:2009-12-1
開本:16開
紙張:膠版紙
印次:1
I S B N:9787564501709
包裝:平裝
內容簡介
本書是全國高等醫藥院校檢驗專業規劃教材《臨床生物化學檢驗》的配套教材,內容緊扣教學大綱和課程基本要求,按課程教學內容的順序編排。全書共分24章,其習題的題型有A型題、B型題、X型題、判斷題、填空題、名詞解釋和問答題等各類考試中出現的題型,每題附有答案和解析,有利於提高學習與複習的效率。附送光碟包含教學課件與電子自測習題集,內容重點突出,易學易用,能充分滿足教學和學習的需要。
本書可供全國高等醫藥院校醫學檢驗及相關專業本科、專科和成人教育(專升本)師生使用,也可供檢驗醫學各級各類專業考試廣大應試人員學習、複習與自測。
目錄
第一章 緒論
第二章 臨床生物化學檢驗基本知識
第三章 臨床生物化學診斷試驗的性能基礎與評價
第四章 臨床酶學檢驗技術
第五章 代謝物酶法分析技術
第六章 臨床生物化學檢驗的方法與試劑盒
第七章 臨床專用生化分析儀分析技術
第八章 自動生化分析儀分析技術
第九章 治療藥物監測
第十章 血漿蛋白質與含氮化合物的代謝紊亂
第十一章 糖代謝紊亂
第十二章 脂蛋白代謝紊亂
第十三章 體液和酸鹼平衡紊亂
第十四章 微量元素與維生素代謝紊亂
第十五章 骨代謝異常的生物化學診斷
第十六章 肝膽疾病的生物化學診斷
第十七章 腎臟疾病的生物化學診斷
第十八章 心血管疾病的生物化學診斷
第十九章 內分泌疾病的生物化學診斷
第二十章 胃腸胰疾病的生物化學診斷
第二十一章 神經與精神疾病的生物化學診斷
第二十二章 妊娠期疾病的生物化學診斷
第二十三章 氧化應激的生物化學診斷
第二十四章 腫瘤的生物化學診斷
附錄 模擬試卷
圖書4信息
編輯推薦
《多元統計分析》是由科學出版計出版的。
文摘
插圖:
序言
作者從20世紀80年代末便從事有關生物數學、數量遺傳學和群體遺傳學等方面的研究生教學工作,後來又承擔了遺傳育種和繁殖專業的碩士生、博士生及套用數學碩士生的培養工作。在長期的科研和教學中,作者思考著農業科學的發展和數學發展的關係問題,因為這個問題直接關係著解決農、林院校研究生數學教學的內容和體系問題。
農業科學是現代科學技術中套用最廣闊、最活躍、最富挑戰性的領域之一,追根溯源,它與數學的發展,尤其與統計學的發展,具有同步性。數學與農業、管理的關係是從人類計數開始的,正如管仲所說“不明於計數,猶如無舟楫欲經於水,險也”。近代農業套用數學是由生物、工程和經濟等科學的進步而發展的。隨著19世紀初近代生物學和經濟統計學的進步,導致了20世紀初遺傳學、經濟學和數學的融合和交叉。生物學家認為“生物學”(biology)這個詞來源於希臘文oiooto(生命),這門學科由於套用了數學,獲得了第二次生命。列寧認為“統計學家和經濟學家各走各的路,那么他們兩者都不能獲得滿意的結果”。20世紀初學科間的融合和以後的發展,使農業套用數學形成了與生物數學、經濟數學、工業數學相平行而互相交融的發展局面。從與農業科學交叉的意義上看,有數量分類學、群體遺傳學、數量遺傳學、數量生態學、數量生理學、數量經濟學、生物信息學、農業系統工程學等。從數學方法上講,有統計學、資訊理論、系統論、控制論、生物方程、運籌學等。概括起來,農業套用數學是農業領域中可套用的數學。從含義上講,有三個方面:一是套用數學知識來解決農業中的實際問題,以求實效,它包括為此而建立的數學模型、計算機模擬法研製等;二是與農業科學相交叉,形成新的學科。如群體遺傳學、生物信息學等;三是從農業科學中提煉出數學問題進行研究,從而發展數學理論。如基因如何從時間、空間上來精細地控制發育過程等。
從農業科學的研究特點上看,它是以實驗和調查為前提的研究過程。首先是根據研究目的進行周密而審慎的試驗設計或抽樣設計,通過實施而得到數據,如孟德爾的豌豆實驗、摩爾根的果蠅實驗、田間調查等。然後通過試驗設計和抽樣設計的數學模型,進行分析而得到研究結論,其中包括了刻畫指標之間關係的數學模型研究。在研究過程中,數學方法起到了把實驗數據轉化為研究結論的作用,如試驗設計的數學模型起到了把處理轉化為輸出指標的作用。又如把樣品的指標觀察值轉化為分類的結果等。