基本函式空間K

設K（或記為）是Rn上無限次可微而且有緊支集的函式全體，在通常的線性運算下成為線性空間。

簡介

基本函式空間K是一類測試函式。

線性空間

基本函式空間K

設φ是定義在n維歐幾里得空間R 上的函式，稱的閉包為φ的支集，記為supp φ。

基本函式空間K

設 為非負整數組，記

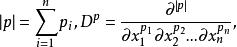基本函式空間K

當p=0時，表示不對x求偏導。特別地，記0=(0,0,...,0)，D φ=φ。

設K（或記為）是R 上無限次可微而且有緊支集的函式全體，在通常的線性運算下成為線性空間。

定義

設函式列{φ}⊂K，q∈K，如果：

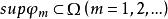基本函式空間K

1.存在有界集s，使得，即{φ}的支集一致有界；

2.對任何p，{D φ}在R 上一致收斂於D φ，則稱{φ}在K中收斂於φ，記為

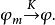基本函式空間K

按上述線性運算和極限運算，稱K是一個基本函式空間，而K中每個函式為基本函式或測試函式。

性質

基本函式空間K

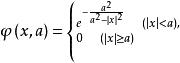基本函式空間K

K是非空的，例如對任何a>0，是 K 中的函式，其中

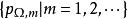基本函式空間K

設Ω 是 R 中的有界閉集，K中支集包含在Ω 中的函式全體記為K，它是線性空間，且按半範數族 成為局部凸拓撲線性空間，其中

基本函式空間K

基本函式空間 K 恰好是一切K的嚴格歸納極限。