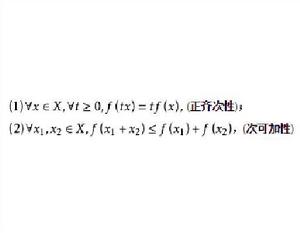基本介紹
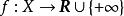 次線性函式
次線性函式有一類特別重要的凸函式 ,稱為 次線性函式,它滿足
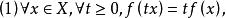 次線性函式
次線性函式( 正齊次性);
 次線性函式
次線性函式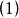 次線性函式
次線性函式,( 次可加性)。
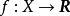 次線性函式
次線性函式 次線性函式
次線性函式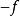 次線性函式
次線性函式 次線性函式
次線性函式任何線性形式(函式)當然都是 次線性函式。反之,易證:如果 ,且 和 都是次線性函式,那么 一定是線性函式。
相關性質
 次線性函式
次線性函式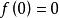 次線性函式
次線性函式次線性函式必定是凸函式;於是次線性函式本質上也將是仿射函式族的上包絡。但由於次線性函式 還一定滿足 等條件,我們還能得到更強的結果。
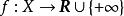 次線性函式
次線性函式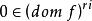 次線性函式
次線性函式 次線性函式
次線性函式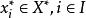 次線性函式
次線性函式命題1設線性空間X上的函式 ,且 ,那么 是次線性函式的充要條件為:存在一族線性形式 ,使得
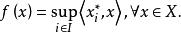 次線性函式
次線性函式 次線性函式
次線性函式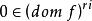 次線性函式
次線性函式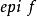 次線性函式
次線性函式推論設 是滿足 的次線性函式,那么 是代數閉凸集。
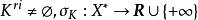 次線性函式
次線性函式定理 設K為線性空間X中的集合,且 是它的承托函式,即
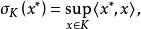 次線性函式
次線性函式那么
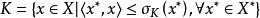 次線性函式
次線性函式的充要條件為:K是代數閉凸集。
Minkowski函式
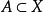 次線性函式
次線性函式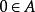 次線性函式
次線性函式非負的次線性函式稱為Minkowski函式,這種函式與包含原點的凸集緊密相關,設 為凸集,且 ,令
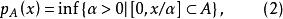 次線性函式
次線性函式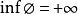 次線性函式
次線性函式這裡規定 ,於是有:
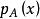 次線性函式
次線性函式命題2 是Minkowski函式。
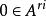 次線性函式
次線性函式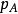 次線性函式
次線性函式命題3 設A為X中的凸集,且 , 如,式(2)所定義,那么
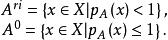 次線性函式
次線性函式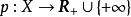 次線性函式
次線性函式命題4設 為Minkowski函式,凸集A滿足
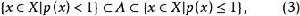 次線性函式
次線性函式那么必定有
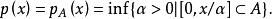 次線性函式
次線性函式命題3把一個相對代數內部非空的凸集與一個Minkowski函式聯繫起來,且它的相對代數內部與代數閉包也都可用這個Minkowski函式表示,命題4又說明這樣的Minkowski函式聯繫的是一族有相同的相對代數內部和代數閉包的凸集。值得注意的是:命題4中並無A的相對代數內部包含原點的要求,於是式(3)的兩端又可看作相對代數內部和代數閉包概念的某種推廣(這裡用A的錐包代替A的仿射包來考慮)。
舉例
每個(半)範數是一個次線性函式。 相反的情況是不正確的,因為(半)規範可以在任何欄位(不一定是有序的)上具有其域向量空間,並且必須具有R作為其代碼域。
範數,是具有“長度”概念的函式。線上性代數、泛函分析及相關的數學領域,範數是一個函式,是矢量空間內的所有矢量賦予非零的正長度或大小。半範數可以為非零的矢量賦予零長度。
定義範數的矢量空間是賦范矢量空間;同樣,定義半範數的矢量空間就是賦半范矢量空間。
在二維的歐氏空間R中定義歐氏範數,在該矢量空間中,元素被畫成一個從原點出發的帶有箭頭的有向線段,每一個矢量的有向線段的長度即為該矢量的歐氏範數。