坎托羅維奇法
正文
求解彈性力學問題的一種近似方法,是蘇聯的Л.В.坎托羅維奇於1933年提出的,故名。此法的要點是:先假定位移分量沿一些方向的變化模式,然後利用彈性力學虛功原理,求出位移分量沿另一些方向的變化。例如,對於薄板的彎曲問題,可先假設薄板撓度ω沿板平面內x、y兩方向的變化為可分離變數的形式,即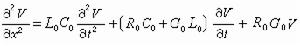
坎托羅維奇法,求解彈性力學問題的一種近似方法,是蘇聯的Л.В.坎托羅維奇於1933年提出的,因此命名。
坎托羅維奇,男,出生於1877年,法學家。曾在德國弗賴堡大學、基爾大學、英國牛津大學、劍橋大學任教,倡導社會學法學派。社會學法學派和自由法學派在歐洲的主...
人物名稱 生平介紹坎托羅維奇,H. 正文德國法學家,社會學法學派和自由法學派...漏洞等情況下進行。 坎托羅維奇的自由法學說與美國現實主義法學派的觀點...》一書中,坎托羅維奇分析了什麼是法,特別是法與其他規範的區別。他為法下...
坎托羅維奇,H. 正文 配圖 相關連線赫爾曼·坎托羅維奇(Kantorouicz,Hermann,1877年11月18日~1940年2月12日)德國法學家,倡導社會學法學派。社會學法學派和自...
諾維奇,英文名Norwich,又被翻譯成:諾里奇。諾維奇(Norwich)是英國東安格里亞地區的中心城市。兩百年前,諾維奇是僅次於倫敦的英格蘭第二大城市...
隊徽發展 球隊戰術特點 球隊歷史 戰隊陣容 戰隊榮譽科托爾(黑山語:Котор ,克羅地亞語:Kotor,拉丁語: Acruvium,希臘語:Ασκρηβιον, Askrèvion,義大利語:Càtta...
簡介 歷史沿革 人口組成 姐妹城市 旅遊景點諾維奇城足球俱樂部(Norwich City Football Club) 是位於英格蘭東部諾福克郡諾維奇的職業足球俱樂部,成立於1902年,由於會徽上...
隊徽發展 球隊戰術特點 球隊歷史 戰隊陣容 戰隊榮譽諾維奇城足球俱樂部(Norwich City Football Club) 是位於英格蘭東部諾福克郡諾維奇的職業足球俱樂部,成立於1902年,由於會徽上...
隊徽發展 球隊戰術特點 球隊歷史 戰隊陣容 戰隊榮譽拉米雷斯·桑托斯·多·納斯西門托(Ramires Santos do Nascimento),1987年3月24日出生於巴西里約熱內盧,巴西足球運動員,...
早年經歷 運動生涯 個人生活 生涯數據 獲獎記錄拉米雷斯·桑托斯·多·納斯西門托(Ramires Santos do Nascimento),1987年3月24日出生於巴西里約熱內盧,巴西足球運動員,...
早年經歷 運動生涯 個人生活 生涯數據 獲獎記錄