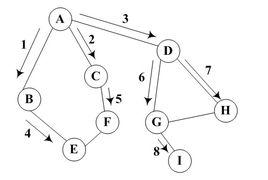
定義
圖遍歷又稱圖的遍歷,屬於數據結構中的內容。指的是從圖中的任一頂點出發,對圖中的所有頂點訪問一次且只訪問一次。圖的遍歷操作和樹的遍歷操作功能相似。圖的遍歷是圖的一種基本操作,圖的許多其它操作都是建立在遍歷操作的基礎之上。
由於圖結構本身的複雜性,所以圖的遍歷操作也較複雜,主要表現在以下四個方面:
① 在圖結構中,沒有一個“自然”的首結點,圖中任意一個頂點都可作為第一個被訪問的結點。
② 在非連通圖中,從一個頂點出發,只能夠訪問它所在的連通分量上的所有頂點,因此,還需考慮如何選取下一個出發點以訪問圖中其餘的連通分量。
③ 在圖結構中,如果有迴路存在,那么一個頂點被訪問之後,有可能沿迴路又回到該頂點。
④ 在圖結構中,一個頂點可以和其它多個頂點相連,當這樣的頂點訪問過後,存在如何選取下一個要訪問的頂點的問題。
分類
圖的遍歷可分為四類:
遍歷完所有的邊而不能有重複,即所謂“一筆畫問題”或“歐拉路徑”;
遍歷完所有的頂點而沒有重複,即所謂“哈密爾頓問題”。
遍歷完所有的邊而可以有重複,即所謂“中國郵遞員問題”;
遍歷完所有的頂點而可以重複,即所謂“旅行推銷員問題”。
對於第一和第三類問題已經得到了完滿的解決,而第二和第四類問題則只得到了部分解決。
第一類問題就是研究所謂的歐拉圖的性質,而第二類問題則是研究所謂的哈密爾頓圖的性質。
算法
圖的遍歷方法目前有深度優先搜尋法和廣度(寬度)優先搜尋法兩種算法。
深度優先搜尋法
深度優先搜尋法是樹的先根遍歷的推廣,它的基本思想是:從圖G的某個頂點v0齣發,訪問v0,然後選擇一個與v0相鄰且沒被訪問過的頂點vi訪問,再從vi出發選擇一個與vi相鄰且未被訪問的頂點vj進行訪問,依次繼續。如果當前被訪問過的頂點的所有鄰接頂點都已被訪問,則退回到已被訪問的頂點序列中最後一個擁有未被訪問的相鄰頂點的頂點w,從w出發按同樣的方法向前遍歷,直到圖中所有頂點都被訪問。其遞歸算法如下:
Boolean visited[MAX_VERTEX_NUM]; //訪問標誌數組
Status (*VisitFunc)(int v); //VisitFunc是訪問函式,對圖的每個頂點調用該函式
void DFSTraverse (Graph G, Status(*Visit)(int v)){
VisitFunc = Visit;
for(v=0; v<G.vexnum; ++v)
visited[v] = FALSE; //訪問標誌數組初始化
for(v=0; v<G.vexnum; ++v)
if(!visited[v])
DFS(G, v); //對尚未訪問的頂點調用DFS
}
void DFS(Graph G, int v){ //從第v個頂點出發遞歸地深度優先遍歷圖G
visited[v]=TRUE; VisitFunc(v); //訪問第v個頂點
for(w=FirstAdjVex(G,v); w>=0; w=NextAdjVex(G,v,w))
//FirstAdjVex返回v的第一個鄰接頂點,若頂點在G中沒有鄰接頂點,則返回空(0)。
//若w是v的鄰接頂點,NextAdjVex返回v的(相對於w的)下一個鄰接頂點。
//若w是v的最後一個鄰接點,則返回空(0)。
if(!visited[w])
DFS(G, w); //對v的尚未訪問的鄰接頂點w調用DFS
}
廣度優先搜尋法
圖的廣度優先搜尋是樹的按層次遍歷的推廣,它的基本思想是:首先訪問初始點vi,並將其標記為已訪問過,接著訪問vi的所有未被訪問過的鄰接點vi1,vi2,…, vi t,並均標記已訪問過,然後再按照vi1,vi2,…, vi t的次序,訪問每一個頂點的所有未被訪問過的鄰接點,並均標記為已訪問過,依次類推,直到圖中所有和初始點vi有路徑相通的頂點都被訪問過為止。其非遞歸算法如下:
Boolean visited[MAX_VERTEX_NUM]; //訪問標誌數組
Status (*VisitFunc)(int v); //VisitFunc是訪問函式,對圖的每個頂點調用該函式
void BFSTraverse (Graph G, Status(*Visit)(int v)){
VisitFunc = Visit;
for(v=0; v<G.vexnum, ++v)
visited[v] = FALSE;
initQueue(Q); //置空輔助佇列Q
for(v=0; v<G.vexnum; ++v)
if(!visited[v]){
visited[v]=TRUE; VisitFunc(v);
EnQueue(Q, v); //v入佇列
while(!QueueEmpty(Q)){
DeQueue(Q, u); //隊頭元素出隊並置為u
for(w=FirstAdjVex(G,u); w>=0; w=NextAdjVex(G,u,w))
if(!Visited[w]){ //w為u的尚未訪問的鄰接頂點
Visited[w]=TRUE; VisitFunc(w);
EnQueue(Q, w);
}
}
}
}
相關代碼
C++語言代碼
#include"stdio.h"
#include"string.h"
#include"stdlib.h"
#include"math.h"
#define MAX_INT 1000
#define MAX_VERTEX_NUM 20
#define MAX_QUEUE_NUMBER 20
typedef struct ArcNode
{
int adjvex;
double adj;
struct ArcNode *nextarc;
}ArcNode;
typedef struct VexNode
{
char szName[40];
ArcNode *firstarc;
}VexNode,AdjList[MAX_VERTEX_NUM];
typedef struct
{
AdjList vexs;
int vexnum,arcnum;
}Net;
//定義佇列
typedef struct{
int *elem;
int front, rear;
}Queue;
void InitQueue(Queue &Q)
{
Q.elem = new int[MAX_QUEUE_NUMBER];
Q.front = Q.rear = 0;
}
int EmptyQueue(Queue Q)
{
if(Q.front==Q.rear)
return 0;
else
return 1;
}
void DestroyQueue(Queue &Q){
delete []Q.elem;
Q.front = Q.rear = 0;
}
void EnterQueue(Queue &Q, int e)
{
if((Q.rear + 1)%MAX_QUEUE_NUMBER != Q.front)
Q.elem[Q.rear ]= e;
else
printf("佇列滿!\n");
Q.rear = (Q.rear + 1)%MAX_QUEUE_NUMBER;
}
void LeaveQueue(Queue &Q, int &e)
{
if(Q.rear != Q.front)
e = Q.elem[Q.front];
else
printf("佇列空!\n");
Q.front = (Q.front+1)%MAX_QUEUE_NUMBER;
}
int LocateVex(Net ga,char *name)
{
int i;
for(i=0;i<ga.vexnum;i++)
if(strcmp(name,ga.vexs[i].szName)==0)
return i;
return -1;
}
void crt_net(Net &ga)
{
ArcNode *p;
char name1[40],name2[40];
int i,j,k;
double w;
printf("請輸入頂點數和弧數:");
scanf("%d%d",&ga.vexnum,&ga.arcnum);
printf("請依次輸入頂點名:\n");
for(i=0;i<ga.vexnum;i++)
{
scanf("%s",ga.vexs[i].szName);
ga.vexs[i].firstarc=NULL;
}
for(k=0;k<ga.arcnum;k++)
{
printf("請輸入相鄰的兩個定點和權值:");
scanf("%s%s%lf",name1,name2,&w);
i=LocateVex(ga,name1);
j=LocateVex(ga,name2);
p=new ArcNode;
p->adjvex=j;
p->adj=w;
p->nextarc=ga.vexs[i].firstarc;
ga.vexs[i].firstarc=p;
}
}
void DFS(Net ga,char *name,int *visited)
{
int v,w;
ArcNode *p;
v=LocateVex(ga,name);
visited[v]=1;
printf("%s ",ga.vexs[v].szName);
p=ga.vexs[v].firstarc;
while(p!=NULL)
{
w=p->adjvex;
if(visited[w]==0)
DFS(ga,ga.vexs[w].szName,visited);
p=p->nextarc;
}
}
void DFSTravel(Net ga,char *name)
{
int v,k=0;
int visited[20];
for(v=0;v<ga.vexnum;v++)
visited[v]=0;
for(v=LocateVex(ga,name);k!=2;v=(v+1)%(ga.vexnum-1))
{
if(v+1==LocateVex(ga,name))
k++;
if(visited[v]==0)
DFS(ga,ga.vexs[v].szName,visited);
}
}
void BFSTravel(Net ga,char *name)
{
ArcNode *p;
int v,w,u,k=0;
Queue Q;
int visited[20];
for(v=0;v<ga.vexnum;v++)
visited[v]=0;
InitQueue(Q);
for(v=LocateVex(ga,name);k!=2;v=(v+1)%(ga.vexnum-1))
{
if(v+1==LocateVex(ga,name))
k++;
if(visited[v]==0)
{
visited[v]=1;
printf("%s ",ga.vexs[v].szName);
EnterQueue(Q,v);
while(EmptyQueue(Q)!=0)
{
LeaveQueue(Q,u);
p=ga.vexs[u].firstarc;
while(p!=NULL)
{
w=p->adjvex;
if(visited[w]==0)
{
printf("%s ",ga.vexs[w].szName);
visited[w]=1;
EnterQueue(Q,w);
}
p=p->nextarc;
}
}
}
}
}
void main()
{
char name[40];
Net ga;
crt_net(ga);
printf("請輸入深度優先遍歷開始點的名:");
scanf("%s",name);
printf("深度優先遍歷:");
DFSTravel(ga,name);
printf("\n");
printf("請輸入廣度優先遍歷開始點的名:");
scanf("%s",name);
printf("廣度優先遍歷:");
BFSTravel(ga,name);
printf("\n");
}