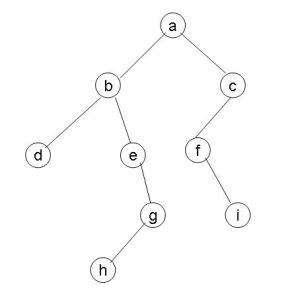
簡介
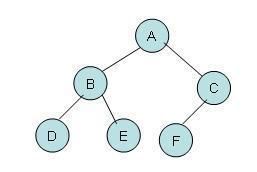 二叉樹
二叉樹若二叉樹為空則結束返回,
否則:
(1)後序遍歷左子樹
(2)後序遍歷右子樹(3)訪問根結點
後序遍歷結果:DEBFCA
已知前序遍歷和中序遍歷,就能確定後序遍歷。
遞歸算法
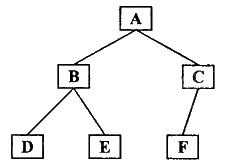 遞歸算法
遞歸算法(1)若二叉樹為空,結束
(2)後序遍歷左子樹
(3)後序遍歷右子樹
(4)訪問根結點遍歷結果:DEBFCA
算法1
PROCEDUREPOSTRAV(BT)IFBT<>0THEN
{POSTRAV(L(BT))
POSTRAV(R(BT))
OUTPUTV(BT)}
RETURN
算法2(C語言)
structbtnode{intd;
structbtnode*lchild;
structbtnode*rchild;};
voidpostrav(structbtnode*bt)
{if(bt!=NULL)
{postrav(bt->lchild);
postrav(bt->rchild);
printf("%d",bt->d);}}
算法3(Pascal語言)
procedurelast(bt:tree);begin
ifbt<>nilthenbegin
last(bt^.left);
last(bt^.right);
write(bt^.data);
end;
end;
算法4(Java語言)
publicclassTreeNode{intval;
TreeNodeleft;
TreeNoderight;
TreeNode(intx){val=x;}}
publicvoidpostOrder(TreeNodebiTree){
TreeNodeleftTree=biTree.left;
if(leftTree!=null){
postOrder(leftTree);}
TreeNoderightTree=biTree.right;
if(rightTree!=null){
postOrder(rightTree);}
System.out.printf(biTree.val+"");}
非遞歸算法
算法核心思想
首先要搞清楚先序、中序、後序的非遞歸算法共同之處:用棧來保存先前走過的路徑,以便可以在訪問完子樹後,可以利用棧中的信息,回退到當前節點的雙親節點,進行下一步操作。後序遍歷的非遞歸算法是三種順序中最複雜的,原因在於,後序遍歷是先訪問左、右子樹,再訪問根節點,而在非遞歸算法中,利用棧回退到時,並不知道是從左子樹回退到根節點,還是從右子樹回退到根節點,如果從左子樹回退到根節點,此時就應該去訪問右子樹,而如果從右子樹回退到根節點,此時就應該訪問根節點。所以相比前序和後序,必須得在壓棧時添加信息,以便在退棧時可以知道是從左子樹返回,還是從右子樹返回進而決定下一步的操作。
算法1(c語言)
voidpostrav1(structbtnode*bt)
{
structbtnode*p;
struct
{
structbtnode*pt;
inttag;
}st[MaxSize];
inttop=-1;
top++;
st[top].pt=bt;
st[top].tag=1;
while(top>-1)/*棧不為空*/
{
if(st[top].tag==1)/*不能直接訪問的情況*/
{
p=st[top].pt;
top--;
if(p!=NULL)
{
top++;/*根結點*/
st[top].pt=p;
st[top].tag=0;
top++;/*右孩子結點*/
st[top].pt=p->p->rchild;
st[top].tag=1;
top++;/*左孩子結點*/
st[top].pt=p->lchild;
st[top].tag=1;
}
}
}
if(st[top].tag==0)/*直接訪問的情況*/
{
printf("%d",st[top].pt->d);
top--;}}
算法2
voidpostrav2(structbtnode*bt)
{
structbtnode*st[MaxSize],*p;
intflag,top=-1;
if(bt!=NULL)
{
do
{
while(bt!=NULL)
{
top++;
st[top]=bt;
bt=bt->lchild;
}
p=NULL;
flag=1;
while(top!=-1&&flag)
{
bt=st[top];
if(bt->rchild==p)
{
printf("%d",bt->d);
top--;
p=bt;
}
else
{
bt=bt->rchild;
flag=0;
}
}
}while(top!=-1)
printf("\n");
}
}