定義
樹的這3種遍歷方式可遞歸地定義如下:
如果T是一棵空樹,那么對T進行前序遍歷、中序遍歷和後序遍歷都是空操作,得到的列表為空表。
如果T是一棵單結點樹,那么對T進行前序遍歷、中序遍歷和後序遍歷都只訪問這個結點。這個結點本身就是要得到的相應列表。
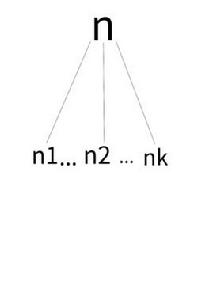
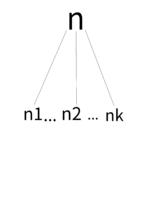
否則,設T如圖6所示,它以n為樹根,樹根的子樹從左到右依次為T1,T2,..,Tk,那么有:
對T進行前序遍歷是先訪問樹根n,然後依次前序遍歷T1,T2,..,Tk。
對T進行中序遍歷是先中序遍歷T1,然後訪問樹根n,接著依次對T2,T3,..,Tk進行中序遍歷。
對T進行後序遍歷是先依次對T1,T2,..,Tk進行後序遍歷,最後訪問樹根n。
 樹圖結構
樹圖結構前序遍歷和中序遍歷可形式地依次描述如下 :
三種遍歷可以形式地描述如下,其中用到了樹的ADT操作:
Procedure Preorder_Traversal(v:NodeType); {前序遍歷算法}
begin
Visite(v); {訪問節點v}
i:=Leftmost_Child(v);
while i<>∧ do
begin
Preorder_Traversal(i);{從左到右依次訪問v的每一個兒子節點i}
i:=Right_Sibling(i);
end;
end;
Procedure Inorder_Traversal(v:NodeType); {中序遍歷算法}
begin
if Leftmost_Child(v)=∧ {判斷v是否是葉節點}
then Visite(v)
else
begin
Inorder_Traversal(Leftmost_Child(v)); {中序遍歷v的左邊第一個兒子節點}
Visite(v); {訪問節點v}
i:=Right_Sibling(Leftmost_Child(v)); {i=v的左邊第二個兒子}
while i<>∧ do
begin
Inorder_Traversal(i);
{從左邊第二個開始到最右邊一個為止依次訪問v的每一個兒子節點i}
i:=Right_Sibling(i);
end;
end;
end;
Procedure Postorder_Traversal(v:NodeType); {後序遍歷算法}
begin
i:=Leftmost_Child(v);
while i<>∧ do
begin
Preorder_Traversal(i);{從左到右依次訪問v的每一個兒子節點i}
i:=Right_Sibling(i);
end;
Visite(v); {訪問節點v}
end;
方法
為了將一棵樹中所有結點按某種次序列表,只須對樹根調用相應過程。例如對圖7中的樹進行前序遍歷、中序遍歷和後序遍歷將分別得到前序列表:A B E F I J
C D G H;中序列表:E B I F J A C G D H;後序列表:E I J F B C G H D A。
下面介紹一種方法可以產生上述3種遍歷方式的結點列表。構想我們從樹根出發,依逆時針方向沿樹的外緣繞行(例如圍繞圖7中的樹繞行的路線如圖8所示)。繞行途中可能多次經過同一結點。如果我們按第一次經過的時間次序將各個結點列表,就可以得到前序列表;如果按最後一次經過的時間次序列表,也就是在即將離開某一結點走向其父親時將該結點列出,就得到後序列表。為了產生中序列表,要將葉結點與內部結點加以區別。葉結點在第一次經過時列出,而內部結點在第二次經過時列出。
在上述3種不同次序的列表方式中,各樹葉之間的相對次序是相同的,它們都按樹葉之間從左到右的次序排列。3種列表方式的差別僅在於內部結點之間以及內部結點與樹葉之間的次序有所不同。
一棵樹進行前序列表或後序列表有助於查詢結點間的祖先子孫關係。假設結點v在後序列表中的序號(整數)為postorder(v),我們稱這個整數為結點v的後序編號。例如在圖7中,結點E,I和J的後序編號分別為1,2和3。
結點的後序編號具有這樣的特點:設結點v的真子孫個數為desc(v),那么在以v為根的子樹中的所有結點的後序編號恰好落在postorder(v)- desc(v)與postorder(v)之間。因此為了檢驗結點x是否為結點y的子孫,我們只要判斷它們的後序編號是否滿足:
postorder(y)-desc(y)≤postorder(x)≤postorder(y)
前序編號也具有類似的性質。