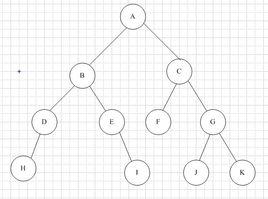
簡介
在計算機科學中,所謂 遍歷(Traversal),是指沿著某條搜尋路線,依次對樹中每個結點均做一次且僅做一次訪問。訪問結點所做的操作依賴於具體的套用問題。遍歷序列是指沿著某條搜尋路線訪問序列中的元素,不同的遍歷方式,其訪問序列中元素的順序是不一樣的,並且和序列的有關性質有關,例如一個給定序列的子序列是從給定序列中去除一些元素,而不改變其他元素之間相對位置而得到的。在數據結構中,套用遍歷序列最多的結構是樹和圖。
二叉樹的遍歷序列
二叉樹的定義
二叉樹(BinaryTree)是一種樹型結構,它的特點是每個節點至多只有兩棵子樹(即二叉樹中不存在度大於2的節點),並且,二叉樹的子樹有左右之分,其次序不能任意顛倒。 二叉樹的五種基本形態:二叉樹可以是空集;根可以有空的左子樹或右子樹;或者左、右子樹皆為空;或左、右子樹均為非空的二叉樹。
遍歷方案
從二叉樹的遞歸定義可知,一棵非空的二叉樹由根結點及左、右子樹這三個基本部分組成。因此,在任一給定結點上,可以按某種次序執行三個操作:
(1)訪問結點本身(N),
(2)遍歷該結點的左子樹(L),
(3)遍歷該結點的右子樹(R)。
以上三種操作有六種執行次序:
NLR、LNR、LRN、NRL、RNL、RLN。
前三種次序與後三種次序對稱,故只討論先左後右的前三種次序。
三種遍歷的命名
根據訪問結點操作發生位置命名:
① NLR:前序遍歷(PreorderTraversal亦稱(先序遍歷))
——訪問結點的操作發生在遍歷其左右子樹之前。
② LNR:中序遍歷(InorderTraversal)
——訪問結點的操作發生在遍歷其左右子樹之中(間)。
③ LRN:後序遍歷(PostorderTraversal)
——訪問結點的操作發生在遍歷其左右子樹之後。
由於被訪問的結點必是某子樹的根,所以N(Node)、L(Left subtlee)和R(Right subtree)又可解釋為根、根的左子樹和根的右子樹。NLR、LNR和LRN分別又稱為先根遍歷、中根遍歷和後根遍歷。
遍歷算法
1. 中序遍歷的遞歸算法定義:
若二叉樹非空,則依次執行如下操作:
(1)遍歷左子樹;
(2)訪問根結點;
(3)遍歷右子樹。
2.先序遍歷的遞歸算法定義:
若二叉樹非空,則依次執行如下操作:
(1) 訪問根結點;
(2) 遍歷左子樹;
(3) 遍歷右子樹。
3.後序遍歷得遞歸算法定義:
若二叉樹非空,則依次執行如下操作:
(1)遍歷左子樹;
(2)遍歷右子樹;
(3)訪問根結點。
中序遍歷的算法實現
用二叉鍊表做為存儲結構,中序遍歷算法可描述為:
void InOrder(BinTree T)
{ //算法里①~⑥是為了說明執行過程加入的標號
① if(T) { // 如果二叉樹非空
② InOrder(T->lchild);
③ printf("%c",T->data); // 訪問結點
④ InOrder(T->rchild);
⑤ }
⑥ } // InOrder
圖的遍歷序列
圖的定義
圖(Graph)是一種複雜的非線性結構。在人工智慧、工程、數學、物理、化學、生物和計算機科學等領域中,圖結構有著廣泛的套用。圖G由兩個集合V和E組成,記為:
G=(V,E)
其中:
V是頂點的有窮非空集合,
E是V中頂點偶對(稱為邊)的有窮集。
通常,也將圖G的頂點集和邊集分別記為V(G)和E(G)。E(G)可以是空集。若E(G)為空,則圖G只有頂點而沒有邊。
深度優先遍歷序列
對圖進行深度優先遍歷時,按訪問頂點的先後次序得到的頂點序列稱為該圖的深度優先遍歷序列,或簡稱為DFS序列。
(1)一個圖的DFS序列不一定惟一當從某頂點x出發搜尋時,若x的鄰接點有多個尚未訪問過,則我們可任選一個訪問之。
(2)源點和存儲結構的內容均已確定的圖的DFS序列惟一
① 鄰接矩陣表示的圖確定源點後,DFS序列惟一
DFSM算法中,當從vi出發搜尋時,是在鄰接矩陣的第i行上從左至右選擇下一個未曾訪問過的鄰接點作為新的出發點,若這樣的鄰接點多於一個,則選中的總是序號較小的那一個。
②只有給出了鄰接表的內容及初始出發點,才能惟一確定其DFS序列
鄰接表作為給定圖的存儲結構時,其表示不惟一。因為鄰接表上邊表里的鄰接點域的內容與建表時的輸入次序相關。因此,只有給出了鄰接表的內容及初始出發點,才能惟一確定其DFS序列。
廣度優先遍歷序列
廣度優先遍歷的遞歸定義
設圖G的初態是所有頂點均未訪問過。在G中任選一頂點v為源點,則廣度優先遍歷可以定義為:首先訪問出發點v,接著依次訪問v的所有鄰接點w1,w2,…,wt,然後再依次訪問與wl,w2,…,wt鄰接的所有未曾訪問過的頂點。依此類推,直至圖中所有和源點v有路徑相通的頂點都已訪問到為止。此時從v開始的搜尋過程結束。
若G是連通圖,則遍歷完成;否則,在圖C中另選一個尚未訪問的頂點作為新源點繼續上述的搜尋過程,直至G中所有頂點均已被訪問為止。
廣度優先遍歷類似於樹的按層次遍歷。採用的搜尋方法的特點是儘可能先對橫向進行搜尋,故稱其為廣度優先搜尋(Breadth-FirstSearch)。相應的遍歷也就自然地稱為廣度優先遍歷。
廣度優先搜尋過程
在廣度優先搜尋過程中,設x和y是兩個相繼要被訪問的未訪問過的頂點。它們的鄰接點分別記為x1,x2,…,xs和y1,y2,…,yt。為確保先訪問的頂點其鄰接點亦先被訪問,在搜尋過程中使用FIFO佇列來保存已訪問過的頂點。當訪問x和y時,這兩個頂點相繼入隊。此後,當x和y相繼出隊時,我們分別從x和y出發搜尋其鄰接點x1,x2,…,xs和y1,y2,…,yt,對其中未訪者進行訪問並將其人隊。這種方法是將每個已訪問的頂點人隊,故保證了每個頂點至多只有一次人隊。
廣度優先搜尋算法
void BFS(ALGraph*G,int k)
{// 以vk為源點對用鄰接表表示的圖G進行廣度優先搜尋
int i;
CirQueue Q; //須將佇列定義中DataType改為int
EdgeNode *p;
InitQueue(&Q);//佇列初始化
//訪問源點vk
printf("visit vertex:%e",G->adjlist[k].vertex);
visited[k]=TRUE;
EnQueue(&Q,k);//vk已訪問,將其人隊。(實際上是將其序號人隊)
while(!QueueEmpty(&Q)){//隊非空則執行
i=DeQueue(&Q); //相當於vi出隊
p=G->adjlist[i].firstedge; //取vi的邊表頭指針
while(p){//依次搜尋vi的鄰接點vj(令p->adjvex=j)
if(!visited[p->adivex]){ //若vj未訪問過
printf("visitvertex:%c",C->adjlistlp->adjvex].vertex); //訪問vj
visited[p->adjvex]=TRUE;
EnQueue(&Q,p->adjvex);//訪問過的vj人隊
}//endif
p=p->next;//找vi的下一鄰接點
}//endwhile
}//endwhile
}//end of BFS