簡介
圖科斯基方程（英文：Teukolsky equation）是康奈爾大學的索爾·圖科斯基（Saul Teukolsky）於二十世紀七十年代創立的克爾度規下的廣義相對論引力場方程。方程的基本思想是在克爾幾何的框架下套用微擾數值求解愛因斯坦場方程，其適用範圍包括各種微擾場：
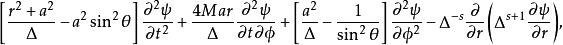圖科斯基方程
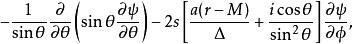圖科斯基方程
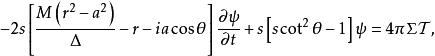圖科斯基方程
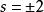圖科斯基方程其中s叫做自旋權重（spin weight），是一個與微擾場的自旋有關的量，在引力場的微擾下；方程中其他物理量的含義請參考克爾度規。
克爾度規
廣義相對論中， 克爾度規（英語：Kerr metric）或稱 克爾真空（英語：Kerr vacuum），描述的一旋轉、球對稱之質量龐大物體（例如：黑洞）周遭真空區域的時空幾何。其為廣義相對論的精確解，故又稱 克爾解；廣義相對論的主導方程——愛因斯坦場方程是非線性的，找出其精確解是相當困難的任務。
克爾度規是史瓦西度規（1915年）的推廣，後者用以描述靜態不旋轉、球對稱且不帶電荷的龐大物體周遭真空區域的時空幾何。在有帶電荷的情形，史瓦西度規轉成雷斯勒-諾德斯特洛姆度規（1916年–1918年）。約瑟夫·冷澤和漢斯·提爾苓曾使用弱場近似方法得到過旋轉軸對稱球狀物體度規的近似解。直到1963年方由羅伊·克爾提出精確解。，但他並沒有給出推導過程。1973年Schiffer等人給出了克爾度規的推導。
克爾度規的帶電荷版本為克爾-紐曼度規（1965年），以上四個相關的解可整理為如下表格：
| 不旋轉 (J= 0) | 旋轉 (J≠ 0) | |
| 不帶電荷 (Q= 0) | 史瓦西度規 | 克爾度規 |
| 帶電荷 (Q≠ 0) | 雷斯勒-諾德斯特洛姆度規 | 克爾-紐曼度規 |
其中 Q代表物體所帶電荷，而 J代表物體的自轉角動量。
愛因斯坦場方程
愛因斯坦重力場方程是一組含有十個方程的方程組，由愛因斯坦於1915年在廣義相對論中提出。此方程組描述了重力是由物質與能量所產生的時空彎曲所造成。也就是說，如同牛頓的萬有引力理論中質量作為重力的來源，亦即有質量就可以產生重力，愛氏的相對論理論更進一步的指出，動量與能量皆可做為重力的來源，並且將“重力場”詮釋成“時空彎曲”。所以當我們知道物質與能量在時空中是如何分布的，就可以計算出時空的曲率，而時空彎曲的結果即是重力。
愛因斯坦重力場方程是用來計算動量與能量所造成的時空曲率，再搭配測地線方程，就可以求出物體在重力場中的運動軌跡。這個想法與電磁學的想法是類似的：當我們知道了空間中的電荷與電流(電磁場的來源)是如何分布的，藉由麥克斯韋方程組，我們可以計算出電場與磁場，再藉由勞倫茲力方程，即可求出帶電粒子在電磁場中的軌跡。
僅在一些簡化的假設下，例如：假設時空是球對稱，此方程組才具有精確解。這些精確解常常被用來模擬許多宇宙中的重力現象，像是黑洞、膨脹宇宙、引力波。
參見
•廣義相對論資源
