簡要說明
 圓系方程
圓系方程在方程(x-a)^2+(y-b)^2=r^2中,若圓心(a,b)為定點,r為參變數,則它表示同心圓的圓系方程.若r是常量,a(或b)為參變數,則它表示半徑相同,圓心在同一直線上(平行於x軸或y軸)的圓系方程.
經過兩圓x^2+y^2+D1x+E1y+F1=0與x^2+y^2+D2x+E2y+F2=0
的交點圓系方程為:
x^2+y^2+D1x+E1y+F1+λ(x^2+y^2+D2x+E2y+F2)=0 (λ≠-1)
經過直線Ax+By+C=0與圓x^2+y^2+Dx+Ey+F=0的交點圓系方程
x^2+y^2+Dx+Ey+F+λ(Ax+By+C)=0
類型1:方程 表示半徑為定長 的圓系
類型2:方程 表示以定點為圓心的同心圓系。
拓展1:方程 表示圓心落在定直線上,半徑為r(r為正數) 的圓系。
拓展2:方程 表示圓心落在任意直線上,半徑為定長 的圓系。
拓展3:方程 表示圓心落在直線 上的圓系。
拓展4:方程 表示圓心落在圓 上,半徑為 的圓系。
類型3:共軸圓系
若⊙C1與⊙C2交於A、B兩點,則直線AB稱為這兩個圓的根軸。經過A、B兩點的所有的圓形成一個圓系,這圓系內任何兩個圓的根軸均為直線AB,因此我們稱這種圓係為共軸圓系。
理解
理解:1.例題:求x+(m+1)y+m=0所過定點
解:可將原式化為x+y+m(y+1)=0
即為x+y=0;y+1=0
解得恆過點(1,-1)
由此我們理解到當除了x,y(為一次冪)還有一未知數m時,依然可求得一定點。
由此可聯想:當有二次方程組x^2+y^2+D1x+E1y+F1=0與x^2+y^2+D2x+E2y+F2=0我們便能求出兩定點。
過一已知圓與一直線的兩個交點的圓系方程為:
x^2+y^2+D1x+E1y+F1+λ(Ax+By+C)=0
理解2:有二次方程組x^2+y^2+D1x+E1y+F1=0 ①式
x^2+y^2+D2x+E2y+F2=0 ②式
①式+②式得x^2+y^2+D1x+E1y+F1+x^2+y^2+D2x+E2y+F2=0
此方程僅符合交點坐標(即帶入交點後成立)
加入參數λ讓方程代表恆過兩點的所有圓。
例題
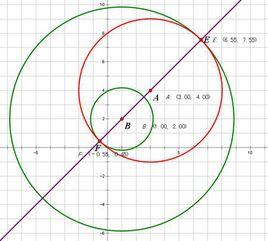
例2:求過兩圓x^2+y^2=25和(x-1)^2+(y-1)^2=16的交點且面積最小的圓的方程。
分析:本題若先聯立方程求交點,再設所求圓方程,尋求各變數關係,求半徑最值,雖然可行,但運算量較大。自然選用過兩圓交點的圓系方程簡便易行。為了避免討論,先求出兩圓公共弦所在直線方程。則問題可轉化為求過兩圓公共弦及圓交點且面積最小的圓的問題。
解:圓x^2+y^2=25和(x-1)^2+(y-1)^2=16的公共弦方程為
x^2+y^2-25-[(x-1)^2+(y-1)^2-16]=0,即2x+2y-9=0
過直線2x+2y-9=0與圓x^2+y^2=25的交點的圓系方程為
x^2+y^2-25+λ(2x+2y-9)=0,即x^2+y^2+2λy+2λx-(9λ+25)=0
依題意,欲使所求圓面積最小,只需圓半徑最小,則兩圓的公共弦必為所求圓的直徑,圓心(-λ,-λ)必在公共弦所在直線2x+2y-9=0上。即-2λ-2λ-9=0,則λ=-9/4
代回圓系方程得所求圓方程(x-9/4)^2+(y-9/4)^2=79/8
總結
圓系方程的主要智慧是將參數的形態放置在圖像中。
參數不僅可在一次環境中表示一個變數,可在直角坐標系中表示一條數軸,還可讓二次圖像以一定的條件變化成無數條函式圖像。
套用
套用一:求圓方程
套用二:證明四點共圓