簡介
在因子分析中,通常只選其中m個(m<p)主因子,即根據變數的相關選出第一主因子ƒ,使其在各變數的公共因子方差中所占的方差貢獻為最大,然後消去這個因子的影響,而從剩餘的相關中,選出與之不相關的因子,使其在各個變數的剩餘因子方差貢獻中為最大,如此往復,直到各個變數公共因子方差被分解完畢為止。
因子分析
[factor analysis]
因子分析是簡化、分析高維數據的一種統計方法。
假定 p 維隨機向量 X=(X,X,...,X) 滿足
 因子載荷
因子載荷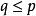 因子載荷
因子載荷f = (f,f,...,f) 是 q 維隨機向量,,滿足 Ef=0,Eff =I,它的分量 f 稱為公共因子(common factor),對 X 的每個分量都起作用。
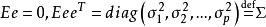 因子載荷
因子載荷e= (e,e,...,e) 是 p 維不可觀測地隨機向量,滿足,且 Efe =0,e 的分量 e稱為特色因子(specific factor),它僅對 X 的分量 X起作用。μ 和 A 為參數矩陣。若 X 滿足上式,則稱隨機向量 X 具有因子結構(factor sturture)。
這時,容易算得
 因子載荷
因子載荷 因子載荷
因子載荷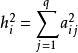 因子載荷
因子載荷矩陣 A 稱為 因子載荷,其元素是第 i 個分量 X 在第 j 個因子 f上的載荷。記,則有
 因子載荷
因子載荷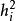 因子載荷
因子載荷由此可見,反應了公共因子對 X的影響,稱為公共因子對 X 的 “貢獻” 。
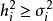 因子載荷
因子載荷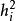 因子載荷
因子載荷 因子載荷
因子載荷當 時,表明公共因子對X的影響大於特殊因子 e的影響,也可以看出反映了X的對公共因子f對 X 的影響也越大,所以 是衡量公共因子重要性的一個尺度。
 因子載荷
因子載荷 因子載荷
因子載荷因子分析的任務就是從 X 的相關矩陣 出發,通過方差最大的正交旋轉,求出矩陣 A 的各列,使相應的“貢獻”有順序。

