概念
定義
 單峰函式
單峰函式 單峰函式
單峰函式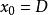 單峰函式
單峰函式 單峰函式
單峰函式 單峰函式
單峰函式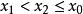 單峰函式
單峰函式設D表示一個實數集合(閉區間,開區間,區間的並,集合等),設是定義在D上的實值函式,如果存在,使得對D中任何冀,,當時,有
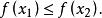 單峰函式
單峰函式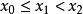 單峰函式
單峰函式當時,
 單峰函式
單峰函式 單峰函式
單峰函式 單峰函式
單峰函式 單峰函式
單峰函式 單峰函式
單峰函式 單峰函式
單峰函式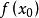 單峰函式
單峰函式 單峰函式
單峰函式 單峰函式
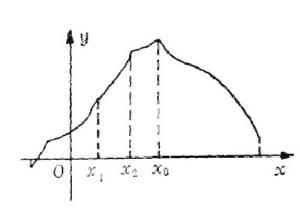
單峰函式那么就說是定義在D上的單峰函式(圖1),換句話說,如果在左邊遞增,在右邊遞減,那么就是D上的 單峰函式,就是在D上的最大值(峰值)稱為 峰值點。
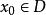 單峰函式
單峰函式 單峰函式
單峰函式 單峰函式
單峰函式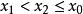 單峰函式
單峰函式類似.如果存在,使得D中任何,,當時,有
 單峰函式
單峰函式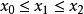 單峰函式
單峰函式當時,有
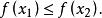 單峰函式
單峰函式 單峰函式
單峰函式 單峰函式
單峰函式那么就說是D上的 單谷函式,稱為 谷值點(圖2)。
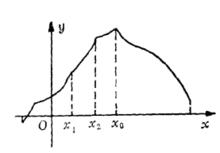 圖1
圖1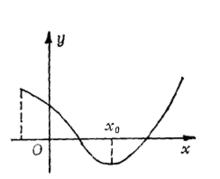 圖2
圖2實例分析
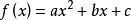 單峰函式
單峰函式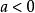 單峰函式
單峰函式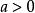 單峰函式
單峰函式例1 二次函式當時,為單峰函式,當時,為單谷函式。
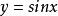 單峰函式
單峰函式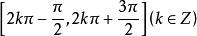 單峰函式
單峰函式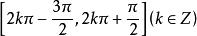 單峰函式
單峰函式 單峰函式
單峰函式例2 函式在為定數)上為單峰函式,而在(均為定數)上為單谷函式。
例3 使用單因素優選法的經驗表明,單因素實驗指標函式大多為單峰(谷)函式。
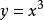 單峰函式
單峰函式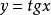 單峰函式
單峰函式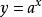 單峰函式
單峰函式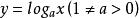 單峰函式
單峰函式例4 函式,,,在整個定義域上不是單峰函式,也不是單谷函式。
由定義可知,單峰函式在定義域上有最大值(峰值),單谷函式有最小值(谷值),這就確定了這函式類在處理極值問題中的地位。
單蜂函式的性質
 單峰函式
單峰函式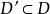 單峰函式
單峰函式 單峰函式
單峰函式由定義可知,在閉區間或有限集合上的單調函式既為單峰函式,又為單谷函式,這樣,就容易證明,對集合D,如是D上單峰函式,,則是D'上的單峰函式,對單谷函式也一樣,歸納起來,單峰(谷)函式有如下性質。
性質1 單峰函式在其定義域的任何子集上,仍為單峰函式,對單谷函式也一樣。
 單峰函式
單峰函式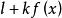 單峰函式
單峰函式 單峰函式
單峰函式 單峰函式
單峰函式 單峰函式
單峰函式 單峰函式
單峰函式性質2 若為單峰(谷)函式,那么(、為常數),當>0時,仍為單峰(谷)函式,當<0時,為單谷(峰)函式,且峰(谷)值點不變。
 單峰函式
單峰函式 單峰函式
單峰函式 單峰函式
單峰函式 單峰函式
單峰函式特別,=0,=-1的情況告訴我們,如為單峰(谷)函式,則一為單谷(峰)函式,因此,在論證有關性質時,只考慮單峰函式就行了。
 單峰函式
單峰函式 單峰函式
單峰函式性質3 如為閉區間D上的凸函式(凹函式),那么必為D上的單谷(峰)函式。
 單峰函式
單峰函式 單峰函式
單峰函式 單峰函式
單峰函式 單峰函式
單峰函式 單峰函式
單峰函式 單峰函式
單峰函式 單峰函式
單峰函式 單峰函式
單峰函式證明:如為D上的單調函式,則為單谷或單峰函式,如不然,則在D上有的部分遞減,有的部分遞增,因此有局部極小(大)點,該局部極小(大)點也是全局極小(大)點,因此,在左邊是減函式,而在右邊為增函式,因此,在D上是單谷(峰)函式,但是反過來不然,這就說明了單峰單谷函式同凸、凹函式的類屬關係。
單峰函式的套用
 單峰函式
單峰函式 單峰函式
單峰函式 單峰函式
單峰函式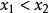 單峰函式
單峰函式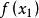 單峰函式
單峰函式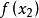 單峰函式
單峰函式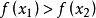 單峰函式
單峰函式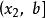 單峰函式
單峰函式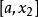 單峰函式
單峰函式 單峰函式
單峰函式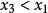 單峰函式
單峰函式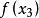 單峰函式
單峰函式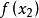 單峰函式
單峰函式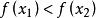 單峰函式
單峰函式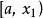 單峰函式
單峰函式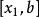 單峰函式
單峰函式 單峰函式
單峰函式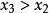 單峰函式
單峰函式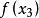 單峰函式
單峰函式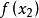 單峰函式
單峰函式 單峰函式
單峰函式我們知道,單峰函式的概念首先是為了解決優選法理論問題的需要而提出來的,而優選法的本質在於用實驗求指標函式(無需知道它的表達式)的極值,而採用的“試一比一去”的程式,就是在實驗區間(即指標函式的定義域)[a,b]內先取兩點(0.618法,分數法,各有特定取法)和,(),通過實驗比較和的大小,如果,則把去掉,留下,其中已有一個試過的點,再按特定方法取,通過實驗比較與的大小,…;如果,則去掉,留下其中包含了已試點,按特定方法取,比較與的大小,…總之,每次去掉壞點(指較小的點)以外的那部分區間。
 單峰函式
單峰函式 單峰函式
單峰函式 單峰函式
單峰函式問題在於這種試驗程式能否保證試驗點序列收斂於最優點?我們知道,一個單峰函式,通過上述程式每次去掉一部分區間以後,性質1保證了在剩下區間上仍是單峰函式,程式可以繼續進行,但是,的峰值點是不是總留在剩下的區間中呢?下面的定理肯定回答了這個問題。
 單峰函式
單峰函式 單峰函式
單峰函式 單峰函式
單峰函式 單峰函式
單峰函式 單峰函式
單峰函式 單峰函式
單峰函式定理 設為[a,b]上的單峰函式,是它的峰值點,設,(<)是[a,b]上任意兩點,那么,
 單峰函式
單峰函式 單峰函式
單峰函式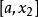 單峰函式
單峰函式若,則在上;
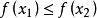 單峰函式
單峰函式 單峰函式
單峰函式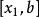 單峰函式
單峰函式若,則在上。