基本介紹
考察一元函式極小化問題
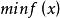 成功失敗法
成功失敗法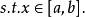 成功失敗法
成功失敗法確定一元函式極值點的數值方法,也即單變數尋優,通常稱為一維搜尋。在最最佳化方法中,一維搜尋雖然簡單,但卻重要,因為多維最最佳化問題的求解一般都伴隨著一系列的一維搜尋。
使用一維搜尋的常用方法有。試探法(成功-失敗法,Fibonacci法,黃金分割法),切線法(一維Newton法),二次插值法(拋物線法)等 。
算法思想
在進行一維搜尋的時候需要確定搜尋區間,也就是包含該問題最優解的一個閉區間,然後在此區間內進行搜尋求解。
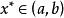 成功失敗法
成功失敗法 成功失敗法
成功失敗法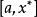 成功失敗法
成功失敗法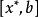 成功失敗法
成功失敗法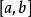 成功失敗法
成功失敗法 成功失敗法
成功失敗法 成功失敗法
成功失敗法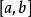 成功失敗法
成功失敗法定義1 若存在 ,使得 在 上嚴格遞減,在 上嚴格遞增,則稱 是 的 下單峰區間, 是 上的 下單峰函式。
顯然,下單峰函式是嚴格凸且有內極小點的函式。
確定下單峰搜尋區間的一個簡單方法就是所謂的 成功-失敗法,該方法不要求函式可微,其基本思想是從一初始點出發,按一定步長尋找目標函式值更優的點,一個方向失敗就退回來,向相反的方向尋找,因此,這是一種試探法 。
算法步驟
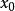 成功失敗法
成功失敗法 成功失敗法
成功失敗法 成功失敗法
成功失敗法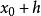 成功失敗法
成功失敗法設初始點為 ,初始步長 ,若 ,則下一步從 出發,加大步長,。繼續向前搜尋,否則反向尋找。算法的具體步驟如下。1
 成功失敗法
成功失敗法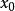 成功失敗法
成功失敗法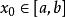 成功失敗法
成功失敗法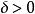 成功失敗法
成功失敗法第一步:選取初始值:給定初始步長 ,初始點 , ,及 。
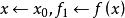 成功失敗法
成功失敗法第二步: 。
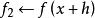 成功失敗法
成功失敗法第三步: 。
 成功失敗法
成功失敗法第四步:比較目標函式值:若 ,則轉第五步;否則,轉第六步。
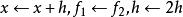 成功失敗法
成功失敗法第五步:加大搜尋步長: ,轉第三步。
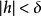 成功失敗法
成功失敗法第六步:判定精度:若 。則轉第七步;否則,轉第八步。
 成功失敗法
成功失敗法第七步:確定最優解: 。
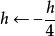 成功失敗法
成功失敗法第八步:反向搜尋: ,轉第三步。
例題解析
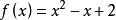 成功失敗法
成功失敗法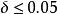 成功失敗法
成功失敗法【例1】求函式 在 內的近似極小點, 。
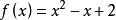 成功失敗法
成功失敗法 成功失敗法
成功失敗法解 顯然 是下單峰函式,取 按成功一失敗法的步驟進行疊代:
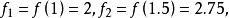 成功失敗法
成功失敗法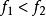 成功失敗法
成功失敗法第一次: 比較得到 。
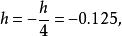 成功失敗法
成功失敗法第二次:取 有
 成功失敗法
成功失敗法 成功失敗法
成功失敗法比較得到 。
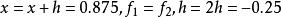 成功失敗法
成功失敗法第三次: ,有
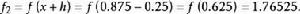 成功失敗法
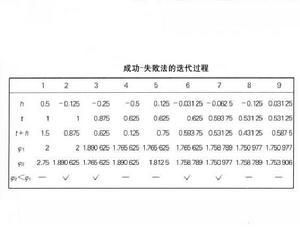
成功失敗法後續的疊代結果見表1。
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| h | 0.5 | -0.125 | -0.25 | 一0.5 | 0.125 | -0.031 25 | -0.062 5 | -0.125 | 0.031 25 |
| x | 1 | 1 | 0.875 | 0.625 | 0.625 | 0.625 | 0.59375 | 0.531 25 | 0.531 25 |
| x+h | 1.5 | 0.875 | 0.625 | 0.125 | 0.75 | 0.59375 | 0.531 25 | 0.431 25 | 0.587 5 |
| f | 2 | 2 | 1.890625 | 1.765625 | 1.765625 | 1.765625 | 1.758789 | 1.750977 | 1.750977 |
| f | 2.75 | 1.890625 | 1.765625 | 1.890 625 | 1.812 5 | 1.7587897 | 1.750977 | 1.758789 | 1.753906 |
| f<f | —— | √ | √ | —— | —— | √ | √ | —— | —— |
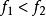 成功失敗法
成功失敗法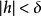 成功失敗法
成功失敗法第九次疊代後, ,並且 ,故,
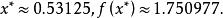 成功失敗法
成功失敗法該問題的精確解為
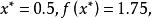 成功失敗法
成功失敗法誤差為6.25%。
成功-失敗法的優點是起步簡單,缺點是不易識別最優解,並且在最優解附近收斂較慢。實際求解中,可以套用該方法將搜尋區間縮小到一定程度後,停止疊代,把原問題轉化為一個搜尋區間較小的最佳化問題,然後,再套用其他最佳化方法進行求解 。