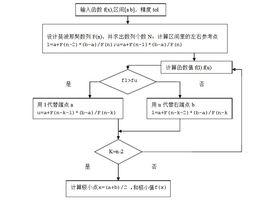
引言
斐波那契搜尋在介紹斐波那契查找算法之前，先介紹一下很它緊密相連的一個概念——黃金分割。黃金比例又稱黃金分割，是指事物各部分間一定的數學比例關係，即將整體一分為二，較大部分與較小部分之比等於整體與較大部分之比，其比值約為1:0.618或1.618:1。0.618被公認為最具有審美意義的比例數字，這個數值的作用不僅僅體現在諸如繪畫、雕塑、音樂、建築等藝術領域，而且在管理、工程設計等方面也有著不可忽視的作用。因此被稱為黃金分割。斐波那契數列：1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89…….（從第三個數開始，後邊每一個數都是前兩個數的和）。然後我們會發現，隨著斐波那契數列的遞增，前後兩個數的比值會越來越接近0.618，利用這個特性，我們就可以將黃金比例運用到查找技術中。
相對於折半查找，一般將待比較的key值與第mid=（low+high）/2位置的元素比較，比較結果分三種情況：
（1）key值與第mid=（low+high）/2相等，mid位置的元素即為所求；
（2）key值大於第mid=（low+high）/2，則令 low=mid+1；
（3）key值小於第mid=（low+high）/2，則令high=mid-1。
斐波那契搜尋也是二分查找的一種提升算法，通過運用黃金比例的概念在數列中選擇查找點進行查找，提高查找效率。同樣地，斐波那契查找也屬於一種有序查找算法。
簡介
斐波那契查找與折半查找很相似，他是根據斐波那契序列的特點對有序表進行分割的。他要求開始表中記錄的個數為某個斐波那契數小1，及n=F(k)-1；開始將k值與第F(k-1)位置的記錄進行比較(及mid=low+F(k-1)-1)，比較結果也分為三種：
（1）相等，則mid位置的元素即為所求；
（2）>，則low=mid+1，k-=2；
說明：low=mid+1說明待查找的元素在[mid+1,high]範圍內，k-=2 說明範圍[mid+1,high]內的元素個數為n-(F(k-1))=Fk-1-F(k-1)=Fk-F(k-1)-1=F(k-2)-1個，所以可以遞歸的套用斐波那契查找。
（3））<，則high=mid-1，k-=1。
說明：low=mid+1說明待查找的元素在[low,mid-1]範圍內，k-=1 說明範圍[low,mid-1]內的元素個數為F(k-1)-1個，所以可以遞歸的套用斐波那契查找。
在最壞情況下，斐波那契查找的時間複雜度還是O(logn)，且其期望複雜度也為O(logn)，但是與折半查找相比，斐波那契查找的優點是它只涉及加法和減法運算，而不用除法，而除法比加減法要占用更多的時間，因此，斐波那契查找的運行時間理論上比折半查找小，但是還是得視具體情況而定。
斐波那契搜尋原理
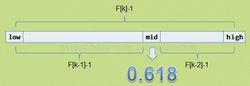
斐波那契搜尋是一種有限區間中單峰函式的搜尋技術。為簡單起見，設此區間為L=[0，1]，記{F}為斐波那契數，
斐波那契搜尋第一次估值點為：
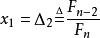斐波那契搜尋和
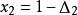斐波那契搜尋其中，1/F應等於或小於搜尋的預期精度。若f(x)>f(x)，則刪去(x，1]，反之刪去[0，x)。以L記刪去的區間，再對留下的區間L取：
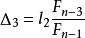斐波那契搜尋
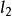斐波那契搜尋
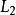斐波那契搜尋其中， 為 的長度。對L重複上述步驟。如此反覆直到：
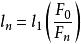斐波那契搜尋已經證明，斐波那契搜尋是一種函式估值次數最少的最優搜尋方法 。
斐波那契搜尋算法實現
斐波那契搜尋算法如下：
