檢驗
單參數假設檢驗問題
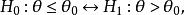 單側檢驗
單側檢驗(1)
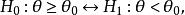 單側檢驗
單側檢驗(2)
稱為單側假設檢驗問題 (one-sided hypothesis test problem)。
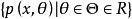 單側檢驗
單側檢驗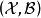 單側檢驗
單側檢驗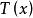 單側檢驗
單側檢驗設 為 上的單參數機率密度族且關於實值統計量 具有非降單調似然比,則關於單側假設檢驗問題(1),有
 單側檢驗
單側檢驗(a)存在水平有 的 UMP 檢驗的檢驗函式
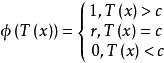 單側檢驗
單側檢驗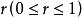 單側檢驗
單側檢驗其中常數 和 c 由下式確定:
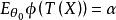 單側檢驗
單側檢驗(b)這個檢驗的勢函式
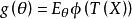 單側檢驗
單側檢驗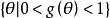 單側檢驗
單側檢驗是非降的,且在集合 上是嚴格增加的。
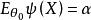 單側檢驗
單側檢驗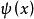 單側檢驗
單側檢驗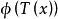 單側檢驗
單側檢驗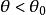 單側檢驗
單側檢驗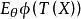 單側檢驗
單側檢驗(c)在一切使得 的檢驗函式 中,由(a)中所確定的檢驗函式 ,使得對任意的 , 都達到最小。
而對單側假設檢驗問題(2),則類似上面的 (a) ,(b),(c) 結論均成立,只需要將(a) 中的第一個式子中的不等號改變方向即可。
意義
當所設H為總體參數等於某一定值,而H為僅從一個方向上偏離此定值者,為單側檢驗。以下是幾種常見的單側檢驗,注意與相應的雙側檢驗分辨。
1.檢驗兩組的差異顯著性時,只考慮A>B之意義,不考慮AB和A<B兩種可能性者,為雙側檢驗。例如,某新藥與一同類的常用藥之療效比較,一般套用雙側檢驗;而含甲藥之某複方與單純甲藥之療效比較,則可以採用單側檢驗。
2.檢驗差值均數的顯著性時,只考慮正值的意義,不考慮負值之可能性者,為單側檢驗(若上述正值和負值之設定相反,亦為單側檢驗);同時考慮包含正值和負值兩個方面的可能性者,為雙側檢驗。例如,試驗某藥是否有降血脂作用,一般應取雙側檢驗;而對傷口之癒合試用某輔助療法時,由於即使不採用任何治療方法傷口亦大多可自愈,故具備了選用單側檢驗的條件。
3.檢驗相關的顯著性時,只考慮正相關的意義,不考慮負相關的可能性者,為單側檢驗(若上述正相關和負相關之設定相反,亦為單側檢驗);同時考慮正相關和負相關兩個可能性者,為雙側檢驗。回歸亦然。例如,兩種試劑同時套用時可能有互動作用,但不明確作用之正負,即產生協同作用抑拮抗作用,一般應採用雙側檢驗;如果有理由只考慮其中之一(設為協同作用)而不必考慮另一作用(為拮抗作用)出現之可能性時,可以選用單側檢驗。
4.為檢驗多個實驗組與一個對照組之差異而進行多重比較時,只考慮在一個方向上的差異,不考慮在另一方向上出現差異之可能性者,為單側檢驗;同時考慮包含兩個相反方向上差異之可能性者,為雙側檢驗。例如,3個實驗組T、T、T與同一個對照組C比較的4組設計中,無疑H:T=C,T=C,T=C;然而H卻有以下兩種狀態:
單側檢驗T>C,T>C,T>C(出現其中1個或2個或全部);
雙側檢驗T≠C,T≠C,T≠C(出現其中1個或2個或全部)。
上述單側檢驗的T也可以是T<C,T<C,T<C。
對於大多數假設檢驗方法,實際套用時都要依據資料之性質及樣本之特徵注意辨識是否適宜採用單側檢驗;如不適宜,則採用雙側檢驗。

