群的子集的乘積
憑藉這個運算我們可以首先解釋商群是什麼,並接著解釋正規子群是什麼:
群 G 的商群是其自身在這個運算下的群 G 的劃分。
它完全由包含 e 的子集所確定。G 的正規子群是在任何這種劃分中包含 e 的集合。在劃分中的子集是這個正規子群的陪集。
群 G 的子群 N 是正規子群,若且唯若陪集等式 aN = Na 對於所有 G 中的 a 都成立。依據上述定義的在子集上的二元運算,G 的正規其群是交換於 G 的所有子集的子群,並指示為 N ⊲ G。 置換於 G 的所有子群的子群叫做可置換子群。
定義
設 N 是群 G 的正規子群。我們定義集合 G/N 是 N 在 G 中的所有左陪集的集合,就是說 G/N = { aN : a∈G }。在 G/N 上的群運算定義如上。換句話說,對於每個 G/N 中 aN 和 bN,aN 和 bN 的乘積是 (aN)(bN)。這個運算是閉合的,因為 (aN)(bN) 實際上是左陪集:
(aN)(bN) = a(Nb)N = a(bN)N = (ab)NN = (ab)N。
N 的正規性被用在了這個等式中。因為 N 的正規性,N 在 G 中的左陪集和右陪集是相等的,所以 G/N 也可以定義為 N 在 G 中所有的右陪集的集合。因為運算是從 G 的子集的乘積得出的,這個運算是良好定義的(不依賴於表示的特定選擇),符合結合律的,並有單位元 N。G/N 的元素 aN 的逆元是 a−1N。
定義的動機
G/N 叫做商群的理由來自整數的除法。在 12 除以 3 的時候得到答案 4 是因為我們可以把 12 個對象重現分組為 3 個對象的 4 個子蒐集。商群出於同樣想法,但用一個群作為最終答案而非一個數,因為群要比對象的隨機蒐集要更有結構。
更細緻的說,在查看 G/N 而 N 是 G 的正規子群的時候,這個群結構形成一種自然“重新分組”。它們是 N 在 G 中陪集。 因為我們從一個群和正規子群得到的最終的商包含比只是陪集的(正常除法所產生的)數目要更多的信息,這裡得到了一個群結構自身。
例子
考慮整數集 Z (在加法下)的群和所有偶數構成的子群 2Z。這是個正規子群,因為 Z 是阿貝爾群。只有兩個陪集: 偶數的集合和奇數的集合;因此商群 Z/2Z 是兩個元素的循環群。這個商群同構於集合 { 0, 1 } 帶有模 2 加法運算的群;非正式的說,有時稱 Z/2Z 等於集合 { 0, 1 } 帶有模 2 加法。
上個例子的稍微一般化。再次考慮整數集 Z 在加法下的群。設 n 是任何正整數。我們考慮由 n 的所有倍數構成的 Z 的子群 nZ。nZ 在 Z 中還是正規子群因為 Z 是阿貝爾群。陪集們是蒐集 {nZ,1+nZ,...,(n−2)+nZ,(n−1)+nZ}。整數 k 屬於陪集 r+nZ,這裡的 r 是 k 除以 n 的餘數。商 Z/nZ 可以被認為模以 n 的“餘數”的群。這是個 n 階循環群。
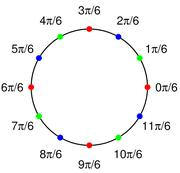
N 在 G 中的陪集考慮複數十二次單位一的根的乘法阿貝爾群 G,它們是在單位圓上的點,它們在右圖中展示為著色的球並在每點上用數標記出它們的幅角。考慮它由單位一的四次根構成的子群 N,在圖中表示為紅色球。這個正規子群把群分解為三個陪集,分別表示為紅色、綠色和藍色。你可以驗證這些陪集形成了三個元素的群(紅色元素和藍色元素的乘積是藍色元素,藍色元素的逆元是綠色元素等等)。因此商群 G/N 是三種顏色元素的群,它又是三個元素的循環群。
考慮實數集 R 在加法下的群,和整數集子群 Z。Z 在 R 中的陪集們是形如 a + Z 的所有集合,這裡 0 ≤ a < 1 是實數。這種陪集的加法是通過做相應的實數的加法,並在結果大於或等於 1 的時候減去 1 完成的。商群 R/Z 同構於圓群 S1,它是絕對值為 1 的複數在乘法下的群,或者說關於原點的二維鏇轉的群,也就是特殊正交群 SO(2)。有一個同構給出為 f(a + Z) = exp(2πia) (參見歐拉恆等式)。
如果 G 是可逆的 3 × 3 實數矩陣的群,而 N 是帶有行列式為 1 的 3 × 3 實數矩陣的子群,那么 N 在 G 中是正規子群(因為它是行列式同態的核)。N 的陪集們是帶有給定行列式的矩陣的集合們,因此 G/N 同構於非零實數的乘法群。
考慮阿貝爾群 Z4 = Z/4Z (也就是集合 { 0, 1, 2, 3 } 帶有加法模 4),和它的子群 { 0, 2 }。商群 Z4 / { 0, 2 } 是 { { 0, 2 }, { 1, 3 } }。這是帶有單位元 { 0, 2 } 的群,群運算如 { 0, 2 } + { 1, 3 } = { 1, 3 }。子群 { 0, 2 } 和商群 { { 0, 2 }, { 1, 3 } } 同構於 Z2。
考慮乘法群 。第 n 個餘數的集合 N 是 的 ϕ(n) 階乘法子群。則 N 在 G 中是正規子群並且因子群 G/N 有陪集 N, (1+n)N, (1+n)2N,…,(1+n)n−1N。 Pallier加密系統基於了在不知道 n 的因子分解的時候難於確定 G 的隨機元素的陪集的猜想。
性質
商群 G / G 同構於平凡群(只有一個元素的群),而 G / 同構於 G。
G / N 的階定義為等於 [G : N],它是 N 在 G 中的子群的指標(index)。如果 G 是有限的,這個指標還等於 G 的階除以 N 的階。注意 G / N 可以在 G 和 N 二者是無限的時候是有限的(比如 Z / 2Z)。
有一個“自然”滿射群同態 π : G → G / N,把每個 G 的元素 g 映射到 g 所屬於的 N 的陪集上,也就是: π(g) = gN。映射 π 有時叫做“ G 到 G / N 上的規範投影”。它的核是 N。
在包含 N 的 G 的子群和 G / N 的子群之間有一個雙射映射;如果 H 是包含 N 的 G 的子群,則對應的 G / N 的子群是 π(H)。這個映射對於 G 的正規子群和 G / N 也成立,並在格定理中形式化。
商群的一些重要性質記錄在同態基本定理和同構基本定理中。
如果 G 是阿貝爾群、冪零群或可解群,則 G / N 也是。
如果 G 是循環群或有限生成群,則 G / N 也是。
如果 N 被包含在 G 的中心內,則 G 也叫做這個商群的中心擴張。
如果 H 是在有限群 G 中的子群,並且 H 的階是 G 的階的一半,則 H 保證是正規子群,因此 G / H 存在並同構於 C2。這個結果還可以陳述為“任何指標為 2 的子群都是正規子群”,並且它的這種形式還適用於無限群。
所有群都同構於一個自由群的商。
有時但非必然的,群 G 可以從 G / N 和 N 重構為一個直積或半直積。判定何時成立的問題叫做擴張問題。不成立的一個例子如下。Z4 / { 0, 2 } 同構於 Z2,並且還同構於 { 0, 2 },但是唯一的半直積是直積,因為 Z2 只有一個平凡的自同構。所以 Z4 不同於 Z2 × Z2,它不能被重構。
參見
商環,也叫做因子環
群擴張
格定理
商範疇
短正合序列