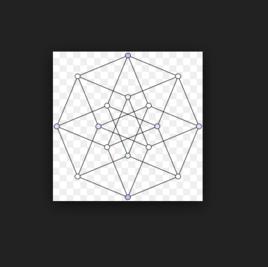
簡介
哈斯圖得名於Helmut Hasse（1898年–1979年）；依據Birkhoff (1948)，這么叫是因為Hasse有效的利用了它們。但是Hasse不是第一個使用它們的人，它們早就出現在如Vogt (1895)中。儘管哈斯圖被設計為手工繪製偏序集合的技術，最近已經使用圖繪製技術自動來生成它們了。
術語“哈斯圖”還可以稱呼作為抽象有向無環圖的傳遞簡約，獨立於這個圖的任何繪製形式。但是這裡不採用這種用法。
圖中的每個結點表示集合A中的一個元素，結點的位置按它們在偏序中的次序從底向上排列。即對任意a，b屬於A，若a≤b且a≠b,則a排在b的下邊。如果a≤b且a≠b，且不存在c∈A滿足a≤c且c≤b，則在a和b之間連一條線。這樣畫出的圖叫哈斯圖，又稱偏序集合圖。
作圖法
（1）以“圓圈”表示元素；
（2）若x≤y,則y畫在x的上層；
（3）若y覆蓋x,則連線；
（4）不可比的元素可畫在同一層。
例題：畫出下列各關係的哈斯圖
1）P={1,2,3,4},<P,≤>的哈斯圖。
2）A={2,3,6,12,24,36},<A,整除>的哈斯圖。
3）A={1,2,3,5,6,10,15,30},<A,整除>的哈斯圖。
解如圖：哈斯圖L-1
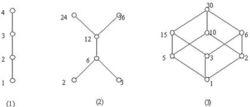哈斯圖L-1例子
{ x, y, z }的冪集按包含偏序排序，有哈斯圖:
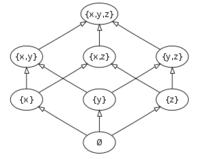哈斯圖所有60的除數的集合A = { 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60 }，按整除性排序，有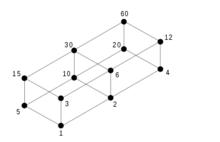哈斯圖:
哈斯圖集合{ 1, 2, 3, 4 }的所有15個劃分，按精細度（就是更細劃分小於更粗劃分）排序，有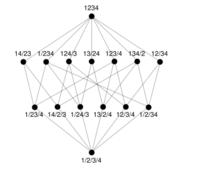哈斯圖:
哈斯圖好的哈斯圖
儘管哈斯圖是簡單的處理有限偏序集的直觀工具，繪製出好的哈斯圖是非常困難的。原因是對於給定偏序集有任意多種可能的繪圖方式。簡單的技術就是開始於這個次序的最小元並逐步增加上更大的元素，這經常產生非常窘迫的結果：很容易丟失了這個次序的對稱性和內部結構。
哈斯圖
哈斯圖下面的例子展示這個問題。考慮集合S = {a, b, c, d}的冪集，就是說S的所有自己的集合，按照子集包含來排序。下面是這個偏序的三個不同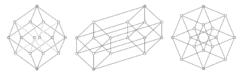哈斯圖:
哈斯圖通過使得在這個冪集中每個集合的y坐標成比例於集合的勢，最左圖示展示了這個冪集是等級偏序集。中間圖示有相同的等級結構，但使得某些邊比其他邊長，它把這個冪集的結構強調為兩個三維立方體的聯合：在兩個立方體中下面的那箇中的頂點表示不包含S的某個特定元素比如d的集合，而上面立方體的頂點表示包含d的集合。最右圖示展示了這個結構的某種內部對稱性。
