合金電子理論

合金電子理論是反映合金中電子運動特點的理論，對晶態的合金來說，能帶論的原理也基本適用，但是合金與純元素相比有根本的區別，即它是由多種不同的原子組成。

合金電子理論

正文

反映合金中電子運動特點的理論。人們對“合金”一詞通常有廣義、狹義兩種理解，狹義的合金指以某金屬元素為基質的固溶體，廣義合金則還包括金屬間化合物以及多相的材料。文獻中“合金的電子理論”多作狹義理解，本條也是這樣。
固體的多電子理論對合金適用。對晶態的合金來說，能帶論的原理也基本適用。但是合金與純元素相比有根本的區別，即它是由多種不同的原子組成。因此合金的電子理論必須分析處理由此而引起的一系列新問題。
先考慮二元稀固溶體的情況。合金的點陣結構與一種元素A相同，且A原子占絕大多數，稱為基質(或溶劑)原子；另一種元素B的原子在合金中很少,稱為雜質（或溶質）原子。在這種合金中，電子運動的性質近似於純元素A，可以把合金電子看成是在A元素點陣的周期場中運動。但是在雜質原子占據的陣點附近，由於B與A不同，周期場受到擾動。這種勢場的擾動引起一些新效應。
首先，合金的傳導電子在雜質附近受到彈性散射。B與A的差異愈大，散射截面也愈大。這種散射是合金在低溫下的剩餘電阻的重要來源（見固體的導電性）。
G.夫里德耳在50年代用自由電子彈性散射的分波法處理過電子被雜質散射的問題，證明雜質彈性散射的分波相移遵守一個求和關係

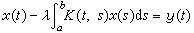。 (1)

式中Z是雜質擾動勢所對應的正電荷數，ηL(EF)是費密能量(見費密面)的角動量量子數 L的分波散射相移。這關係稱夫里德耳求和律。式 (1)右邊這項的意義是摻入雜質後，費密能量以下的總的狀態數和原來自由電子氣的這個總狀態數的差。所以夫里德爾求和律的物理意義是明顯的。某些情況下，雜質引進的態可能是相當局域於雜質原子近旁的。
雜質擾動勢會受到電子氣的禁止。但由於電子的波動性,雜質擾動勢造成的電子散射,相當於在雜質原子附近產生某種駐波,所以,雜質原子周圍的電子密度 ρe(r)隨距離r振盪式地變化。在r比較大處，ρe(r)漸近於

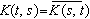。 (2)

式中сF和 嗞F是常數kF是費密波數。這種電子密度振盪已為核磁共振實驗所證實，稱夫里德耳振盪。因此，雜質的禁止勢也和簡單的經典圖像不同，隨距離作振盪變化。
雜質原子也影響合金的電子能譜。最簡單的模型是這樣：合金的電子能譜是在一個假想的純淨晶體勢場中運動電子的能譜,這個假想的純淨晶體勢是基質原子A的勢VA和雜質原子B的勢VB的簡單平均

V0＝xAVA+(1-xA)VB, (3)

式中xA是A原子的百分比。而把實際晶體勢和V0的偏離當作引起散射的根源。這種近似稱虛點陣近似。
在這個意義下，純淨晶體的能帶、布里淵區、能帶填充等概念對合金都可適用。W.休謨—饒塞里曾經從布里淵區的填充情況成功地說明某些合金的結構與成分（平均電子濃度）的關係。
但是，虛點陣近似只是零級近似。1967年以來發展了一種更普遍有效的方法，稱“相干勢近似”方法。根據這個方法，可以自洽地逐級造出一個假想的純淨晶體“勢”(一般說這不是普遍意義下的勢，而是一個算符)，使不同的原子的無序分布所產生的散射效果逐級地統計相消。這種方法在研究合金的各種性質中得到廣泛的套用。
如果組成合金的兩種或幾種不同原子都是作有規則的周期排列，就成了“有序合金”。它實質上是一種金屬間化合物。其傳導電子的運動可用複式點陣的能帶論方法處理。

配圖

相關連線