固體的導電性
正文
不同的固體有不同的導電特性,通常用電導率σ來量度它們的導電能力。電導率的定義是對固體施加的電場強度E與固體內電流密度J的比值。實驗研究指出：在不太強的電場下固體的電導通常服從歐姆定律，即電流密度與電場強度成正比,σ是與電場強度無關的。對於立方晶體或非晶態材料來說,電導率σ是各向同性的，是一個標量。在一般情況下,電導率可能是各向異性的,應該用一個二階張量表示。電導率的單位是歐-1·厘米-1。在許多情況下，電導率的倒數是一個使用起來更方便的量，稱之為電阻率，用ρ表示。根據電導率的數值及其與溫度的依賴關係，大致把固體分為三類：金屬、半導體和絕緣體，下面依次作簡要的說明。
金屬 金屬具有良好的導電性,其電導率在102歐-1·厘米-1以上。金屬中的電流密度J可寫成電子電荷e、電子的平均漂移速度尌和電子濃度n的乘積,即
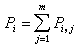。可定義電子平均速度與電場強度E的比值
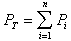為電子遷移率。這樣一來，電導率σ可表為σ＝neμ。在歐姆定律成立的條件下，遷移率μ 與電場強度無關，決定於材料的性質。最早提出的金屬導電理論是P.K.L.德魯德的經典理論。假定金屬中價電子在電場中以同樣方式運動，通過碰撞與組成點陣的離子實交換能量；在兩次碰撞之間，電子被電場加速。電子在碰撞與加速這兩種作用之下，具有一定的平均速度，即一定的遷移率，從而能解釋歐姆定律。類似的考慮套用到熱導理論，可以解釋維德曼－夫蘭茲定律，但德魯德的理論不能解釋金屬電導率與溫度的依賴關係，也不能解釋電子具有幾百個原子間距的長自由程的實驗事實。這些矛盾直到人們用量子理論系統地研究了電子在晶體中運動的能帶理論才得到了解決（見固體的能帶）。能帶論指出，導體、半導體、絕緣體導電性是由於它們的能帶結構不同造成的。金屬導體具有未被電子填滿的能帶，這種帶中的電子能起導電作用，稱為導帶。能帶理論還指出，在嚴格的周期性勢場中，電子可保持處於某個本徵態，且不隨時間改變，也就是說，在嚴格的周期性勢場中電子具有無限長的自由程，不會受到散射。因此，金屬中的電阻並不是由於電子與周期排列的原子的碰撞，而是由於原子在平衡位置附近的熱振動（點陣振動）。使嚴格的周期性勢場遭到破壞，引起散射的結果。考慮了電子與點陣振動的相互作用，即電子－聲子相互作用之後，理論才很好地解釋了電導率與溫度的關係，以及電子具有幾百個原子間距的長自由程的實驗事實。經驗表明，金屬的電阻率與溫度的關係大致上可用一個普適函式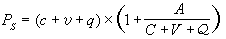 
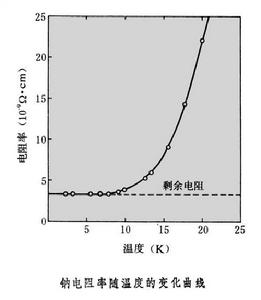
不僅電子與點陣振動相互作用是固體電阻的起因，點陣的不完整性，如缺陷、雜質的存在也破壞了嚴格的周期性勢場，也是電阻的起因。這種原因引起的電阻一般與溫度無關，在低溫下這部分電阻保持不變，不會消失，稱為剩餘電阻。如圖所示，為鈉在低溫時由於點陣缺陷散射機制引起的剩餘電阻。有些金屬和合金，在極低溫度下電阻率會突然降到零，在此轉變溫度下的物質叫做超導體(見超導電性)。
固體的導電性絕緣體 通常把電導率小於10-15歐-1·厘米-1的材料稱作絕緣體。從能帶理論的觀點來看，絕緣體與半導體的區別僅在於絕緣體的禁頻寬度比半導體大，因此絕緣體中載流子濃度非常小，決定了絕緣體的電導率很小。
離子晶體和非導態固體 對某些離子晶體，還存在另一種導電機制──離子導電。它是靠外電場作用下正負離子的移動引起電流的。通常，離子電導率很小。
上述的固體電導都是指晶態固體，對於非晶態固體的電導還有自己的特點，見非晶態材料、非晶態半導體、非晶態電介質。
