固體的能帶
正文
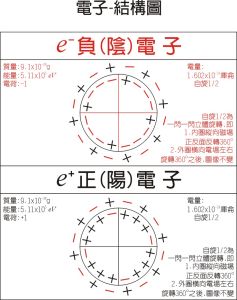 電子-模型圖
電子-模型圖 能帶的基本概念 1928年,F.布洛赫首先運用量子力學的原理來分析晶體中的外層電子的運動。他指出,由於晶體中原子作規則排列,電子是在一個周期勢場中運動。單個電子的波函式嗞(k,R)應該滿足薛丁格方程:
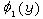 , (1)
, (1)
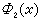 , (2)
, (2)
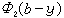 , (3)
, (3)
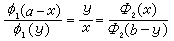 , (4)
, (4)
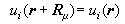 (5)
(5)
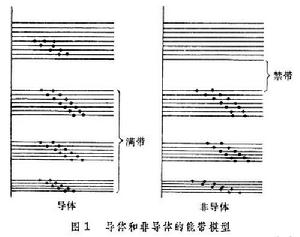
能帶的圖像(圖1)可以說明金屬、半導體和絕緣體的區別。金屬都有部分被電子占據的寬能帶,稱為導帶,在這種能帶中空著的電子態的能量與被占的態相連線,能帶填充情況很容易被電場作用所改變,表現出良好的導電性。絕緣體則是另一種極端情況,電子恰好填滿最低的一系列能帶,其最高的滿帶有時稱為價帶,更高的各能帶都空著。滿帶與空帶之間隔著較寬的禁帶,電場很難使能帶的填充情況改變,因而不產生電流。半導體的能帶填充情況很像絕緣體,但是空導帶與價帶之間的禁帶比絕緣體窄得多,因此可以引入雜質或熱激發,使空導帶出現了少數電子,或價帶中出現少數空穴,或兼有二者,從而有一定的導電性。
 固體的能帶
固體的能帶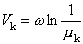 , (6)
, (6)
在能帶的極值點 (k=ko點)附近,價電子狀態的能量可以寫成
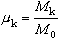 (7)
(7)
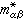
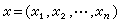 (8)
(8)
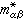 是一個二階張量。在簡單情況下,電子的有效質量m* 為標量
是一個二階張量。在簡單情況下,電子的有效質量m* 為標量 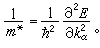 (9)
(9)
固體的許多物理性質,例如電子的比熱容、光吸收和光發射等都同態密度這個函式有密切的關係。態密度函式記作G(E),其定義是在能量E附近單位能量間隔內閃電子態的數目,即
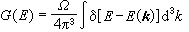 , (10)
, (10)
在外加電場E和磁感應強度場B中,電子態以及電子的平均速度都要變化。在外加場較小的情況,電子的運動服從經典的規律:
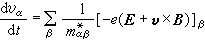 。 (11)
。 (11)
波函式ψi也可以改寫成另一種形式:
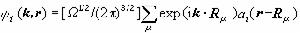 , (12)
, (12)
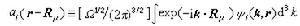 (13)
(13)
計算方法 能帶結構是決定固體各種特殊物理性質的重要因素,對具體材料的能帶進行理論計算和實驗研究一直是半個世紀來固體物理中的一個重要的基礎性課題。到目前為止,人們已對各種簡單金屬、半導體及許多包含 d電子的過渡金屬及其結構比較簡單的化合物的能帶結構作了較可靠的理論計算,與實驗觀測基本相符。近年來,對於f電子的稀土金屬、錒系金屬以及較複雜結構化合物的能帶結構的研究也正在發展中。
嚴格計算三維晶體點陣中的單電子波函式嗞i(k,R)在數學上是極困難的。到目前為止,人們只能求得它的不同精確程度的近似解。下面簡要介紹計算固體能帶的一些理論方法。
緊束縛近似 布洛赫在1928年首先提出一個描寫晶體單電子波函式的緊束縛近似。他考慮電子在陣點Rμ附近主要是受到Rμ原子場的作用。因此仍然可以用在Rμ處的孤立原子中的電子束縛態嗞i(R-Rμ)來近似地描述。然而,電子又可以在整個晶體中作共有化運動,所以對整個波函式 嗞i(k,R)可以取各個陣點原子的束縛態的線性組合來作近似描述,也就是設
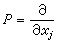 , (14)
, (14)
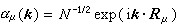 , (15)
, (15)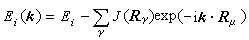 , (16)
, (16)
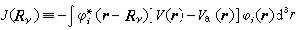 , (17)
, (17)
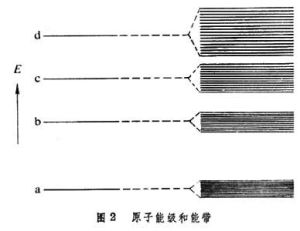
由式 (16)可以看到電子i在晶體中作共有化運動時其能量與孤立原子中的能量Ei有所不同,它隨著波矢k而變化。這樣,對應於孤立原子中的一個量子態i,在固體中有由N個間隔很近的能級組成的“帶”,稱為“能帶”,如圖2所示。能帶的寬度取決於重疊積分J(Rγ),如果各不同原子的波函式之間的重疊愈多,由式(17)可見重疊積分 J(Rγ)的值會愈大,能帶也愈寬。原子內層的電子軌道很小,在不同原子之間很少重疊,因此能帶很窄,而外層電子的軌道在不同原子間重疊很多,所對應的能帶也較寬。在兩個能帶之間沒有電子態的能量區間稱為禁帶。
 固體的能帶
固體的能帶近自由電子近似 也可從另一方向來近似描述固體中的電子運動,把式(1)中的周期勢V(r)分成兩部分:
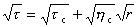 , (18)
, (18)
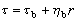 , (19)
, (19)
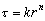 (20)
(20)
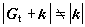
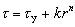 , (21)
, (21)
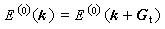 時,上述微擾方法不能使用,需用簡併微擾論來求E(k)。可以證明,在這種波矢k的附近E(k)會出現一個“能隙”(圖3),也就是禁帶。以上這種處理方法稱為近自由電子近似,它所給出的圖像與對簡單金屬的實驗觀測基本相合。
時,上述微擾方法不能使用,需用簡併微擾論來求E(k)。可以證明,在這種波矢k的附近E(k)會出現一個“能隙”(圖3),也就是禁帶。以上這種處理方法稱為近自由電子近似,它所給出的圖像與對簡單金屬的實驗觀測基本相合。 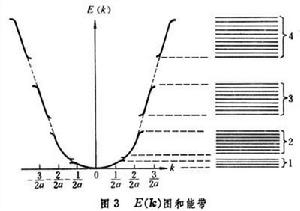 固體的能帶
固體的能帶C.赫林在1940年建議用一套與各原子的內層電子軌道都互相正交的平面波ⅹ(k,r)來代替平面波作為描寫電子波函式嗞(k,r)的基:
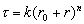 , (22)
, (22)
 (23)
(23)
贗勢法 如果把正交化平面波的式(22)代入晶體的薛丁格方程(1),就可以得出如下的表達式:
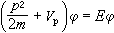 , (24)
, (24)
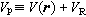 , (25)
, (25)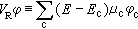 , (26)
, (26)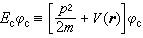 。 (27)
。 (27)
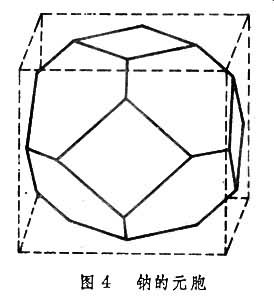
元胞法 E.P.維格納和F.塞茨1933年提出一個計算固體能帶的元胞法。他們把整個晶體劃成分屬於各個原子的許多“元胞”。每個元胞以陣點為中心由與近鄰陣點連線的正交等分面圍成,對體心立方的金屬鈉,元胞形狀如圖4。因為電子之間有很強的互斥作用,可以構想兩個價電子同時處在一個鈉原子元胞內的幾率極小,所以可以近似地假定價電子所感受的勢V(r)只是該元胞中心的離子實勢。而別的元胞的離子實及其餘價電子對它的作用勢幾乎互相抵消。這樣,計算因體鈉中電子波函式的薛丁格方程就和鈉原子問題一樣,所不同的是邊界條件。在固體中必須保證波函式在元胞邊界上平滑連續,並且遵守布洛赫定理。正是這種多邊形邊界條件很難作具體計算。他們對於比較簡單的鈉曾近似地把元胞當作球形來計算,但對比較複雜的金屬就不能這樣作了。
 固體的能帶
固體的能帶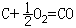 (28)
(28)
