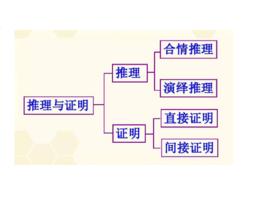
簡介
推理由兩種:論證推理和合情推理。論證推理又稱為演繹推理,它是思維進程中從一般到特殊的推理。這種推理以形式邏輯或論證邏輯為依據,有三段論、關係推理、選言推理和模態推理等推理模式。合情推理一詞來自於Plausible reasoning,又譯為似真推理。這是一種合乎情理的、好像為真的推理。
所謂合情推理,就是一種比較自然的、合乎情理的,似乎為真的推理,它是根據已有的數學事實和正確的數學結論,或以個人數學經驗(數學實驗或實踐)和數學直觀進行推測而得到某些結果的一種推理,常表現為憑直觀和聯想、直觀或直覺等非邏輯思維形式,通過觀察、實驗、歸納、類比,特殊和一般等方法直接獲得某種數學結論。思維的非常規性(如跳躍性)、結論的或然性是其特色。
合情推理是波利亞的“啟發法”(heuristic,即"有助於發現的")中的一個推理模式。波利亞多年深入研究數學問題解決過程(problem solving一般被誤譯為"解題",這裡把它譯為"問題解決")得出的理論成果。波利亞對啟發法解釋道:“現代啟發法力求了解問題解決過程,特別是問題解決過程中典型有用的智力活動.……在這種研究中,我們不應忽視任何一類問題,並且應當找出處理各類問題所共有的特徵來;我們的目的應當是找出一般特徵而與主題無關。”可見波利亞的啟發法講的是問題解決在數學方法論上的共同點。啟發法源於他對問題解決的研究,問題解決就是"在沒有現成的解題方法時尋找一條解題途徑,就是從困難中找到出路,就是尋求一條繞過障礙的道路,由適當的方法達到所要去的而不能立即達到的目的。"這說明波利亞早在50年前就已經把問題和問題解決的主要特徵搞清楚了。
主要特徵
通過對問題解決過程特別是對已有的成功實踐的深入研究,波利亞發現,可以機械地用來解決一切問題的"萬能方法"是不存在的;在問題解決過程中,人們總是針對具體情況,不斷地向自己提出有啟發性的問句,提示,以啟動與推進思維的小船。因此,他試圖總結出一般的方法或模式,這些方法和模式在以後的問題解決活動中可起到啟發和指導的作用。波利亞曾著書給出這樣一些啟發性的模式或方法:分解與組合,笛卡爾模式,遞歸模式,疊加模式,特殊化方法,一般化方法,"從後往前推",設立次目標,合情推理的模式(歸納和類比),畫圖法,"看著未知數",回到定義去,考慮相關的問題,對問題進行變形等等。特別引人注意的是,波利亞把問題和建議按照問題解決過程的4個階段組成了他的"怎樣解題表"。這4個階段依次是:弄清問題,制定計畫,實施計畫和回顧,這就是著名的波利亞問題解決四階段模式。波利亞建議:"只要套用得當,如果你向自己提出表中的這些問題與建議,它們就可以幫助你解決你的問題;而如果你向你的學生提出同樣的問題與建議,你就可以幫助解決他們的問題。"
方法模式
在上述啟發法框架中提到的合情推理的模式(歸納和類比)還須予以解釋,它是指觀察、歸納、類比、實驗、聯想、猜測、矯正與調控等方法。波利亞很早就注意到"數學有兩個側面,……用歐幾里得方式提出來的數學是一門系統的演繹科學;但在創造過程中的數學卻是實驗性的歸納科學。"因此,他明確提出有兩種推理:論證推理可用來確定數學知識,合情推理可用來為猜想提供依據,即波利亞給我們指出數學思維不是純"形式"的,它所涉及的不僅有公理、定理、定義及嚴格的證明,而且還有許許多多其它方面:推廣、歸納、類推以及從具體情況中辨認出或者說抽取出某個數學概念等等,數學教師應使學生了解這些十分重要的"非形式"思維過程。在日常生活中,合情推理幾乎無處不在,比如:"它可能是……"(猜測)",做出來看一看"(實驗)",由上所述可得……"(歸納)",將人心比自心"(類比)",可以想像"(聯想)",實踐是檢驗真理的唯一標準"(檢測)等。
歸納推理
 合情推理
合情推理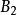 合情推理
合情推理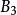 合情推理
合情推理若A,則 , , ,……
 合情推理
合情推理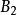 合情推理
合情推理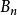 合情推理
合情推理, ,……為真
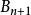 合情推理
合情推理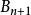 合情推理
合情推理n越大(不真,不像是真的)
——————————————————————
A越可靠(A不真,A極不可靠)
 合情推理
合情推理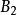 合情推理
合情推理 合情推理
合情推理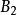 合情推理
合情推理 合情推理
合情推理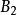 合情推理
合情推理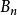 合情推理
合情推理該模型的直觀意義是:若A蘊含,蘊含,……。,,……是更容易證實的,當,,……逐個被證實之後,n越大,A的可靠性也越大。
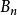 合情推理
合情推理 合情推理
合情推理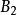 合情推理
合情推理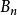 合情推理
合情推理換句話說,當P(/A)=1,P(A∧∧∧……∧)≠0(n≥1)時,有:
 合情推理
合情推理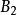 合情推理
合情推理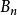 合情推理
合情推理 合情推理
合情推理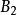 合情推理
合情推理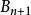 合情推理
合情推理P(A)≤P(A/∧∧……∧))≤P(A/∧∧……∧)。
拓廣推理
若A,則B
B真(A不真條件下B不太真,B意外地被證實)
————————————————————————
A可能真(A很可能真,A非常可靠)
直觀意義:若A蘊含B,且P(B)>0,則P(A)≤P(A/B)。
類比推理
若A類似於B
且A具有性質P
————————————————————————
則B具有性質P'
關係映射便是一種類比推理,如數學中的拉氏變換等。
逆向推理
若A與B不相容
B不可靠
————————————————————————
A較可靠
即,若A與B是不相容的,B的否定性增加了A的可靠性。
肯定推理
若A則B
B
————————————————————————
則A
否定推理
若A則B
非A
————————————————————————
則非B
舉例
在社會生活中,醫生診斷疾病、法官審判案件、軍事家指揮戰爭、人際交往等都套用合情推理。貫徹任何科學發現的思維,也主要是合情推理;量子力學方程是猜出來的;球體公式是阿基米德"稱"出來的;在對熱在金屬中流動的觀察研究中,傅立葉發明了級數;而現代仿生學則是類比推理在科技中套用的傑出成果。由上可以看出,"我們所學到的關於世界的任何新的東西都包含著推理,它是我們日常事務中所關心的僅有的一種推理"。合情推理是各學科之間,社會生活中的文化大使,是現代化社會公民的必備文化素質。
意義
因此加強合情推理的教育將有助於發揮學科的兩個功能,並學會發現和發明的方法。科學思維具有兩重性:一類是進行論證推理的邏輯思維;另一類則是形象思維。形象思維最直接的層面是合情推理,邏輯思維是在"抓到真理"後進行完善和"補行證明"的思維,而合情推理則是"發現真理"的思維。因此,波利亞呼籲:"讓我們教猜想吧!"我國的理科教學,歷來較多強調邏輯推理,而對合情推理有所忽視。再聯想到有關團體對中外學生調查結果顯示的中國學生科學測驗成績較差的信息,不能不使我們感到加強對合情推理能力的培養已是刻不容緩。因此,"既教證明,又教猜想",給合情推理能力的教學以適當的地位,是開發學生創造性素質的需要,是全面提高學生優秀文化素質的需要,是全面開發大腦潛力的需要。我們在教學實踐中認識到加強合情推理的教學,還可以使受教育者將日常事務中積累的經驗,方法用於學習,提高學習的興趣,提高解決問題的能力。而在其中,又將那自然狀態下的合情推理,提高到一個更加合理更加科學的層次,以至成為"科學發現的金鑰匙"。為保證加強合情推理教育的觀念得到落實,並為教師提供一個可操作的教學樣式,我們構建了合情推理教學模式。若在教學中能正確地使用合情推理的教學模式,至少不會削弱學科教學的技術功能,而文化教育功能將得到明顯的加強,學生有效地套用合情推理的技能得到提高,創造能力得到加強,教學質量也將有一定的提高,同時將有一批科研型的教師脫穎而出。
喬治·波利亞
人物簡介
喬治 波利亞(1887-1985),是美籍匈牙利數學家,數學教育家。在數學教育方面他有3部世界名著:《怎樣解題》,《數學與猜想》,《數學的發現———對解題的理解,研究和講授》。這3本書在我國有5個譯本,其中《怎樣解題》發行量已過百萬冊;著名數學家瓦爾登曾高度評價這本書:"每個大學生,每個學者,特別是每個教師都應該讀這本引人入勝的書"。波利亞也謙虛地評價自己說:"在問題解決方面以及講授各種水平的數學方面,作者可以提供一些經驗"。可見波利亞的數學教育思想對世界和我國數學教育的影響非常深遠。
著作
〔美〕喬治.波利亞.怎樣解題〔M〕.閻育蘇譯.北京:科學出版社,1982.
〔美〕喬治.波利亞.數學與猜想(第一卷)〔M〕.李心燦譯.北京:科學出版社,1984.
〔美〕喬治.波利亞.數學與猜想(第二卷)〔M〕.李心燦譯.北京:科學出版社,1984.
〔美〕喬治.波利亞.數學的發現(第一卷)〔M〕.歐陽絳譯.北京:科學出版社,1985.
〔美〕喬治.波利亞.數學的發現(第二卷)〔M〕.劉景麟譯.呼和浩特:內蒙古人民出版社,1981.