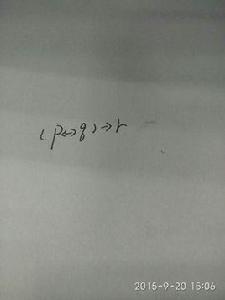相關內容
一個命題公式的合取範式可以通過真值表得到,也可以通過等價變換得到。命題公式還有另一種範式,析取範式。析取範式的定義與合取範式對偶,只要把合取與析取對換就可以由合取項得到析取項,由合取範式得到析取範式。
假設
設A是一個命題公式,A中出現的命題變元為p1,p2,…,pn,以Qi表示pi或┐pi,i=1,…,n。稱Q1∧…∧Qn是p1,…,pn的一個合取項,若干個互不相同的析取項的合取稱為一個合取範式,與命題公式A邏輯等價的合取範式稱為A的合取範式。
合取範式
((p∨q)—>r)—>p
<=>(┐(p∨q)∨r)—>p (消去第一個—>)
<=>┐(┐(p∨q)∨r)∨p (消去第二個—>)
<=>┐((┐p∧┐q)∨r)∨p (┐內移)
<=>((┐┐p∨┐┐q)∧┐r)∨p (┐內移)
<=>((p∨q)∧┐r)∨p (┐消去)
<=>(p∨q∨p)∧(┐r∨p) (∨對∧分配)
這就是所求的原命題公式的合取範式,若再利用交換律和冪等律得:
(p∨q∨p)∧(┐r∨p)
<=>(p∨q)∧(┐r∨p)
可見,(p∨q)∧(┐r∨p)也是原公式的合取範式,這說明一個命題公式的合取範式不是唯一的。