合取範式定理

在布爾邏輯中，如果一個公式是子句的合取，那么它是合取範式(CNF)的。作為規範形式，它在自動定理證明中有用。它類似於在電路理論中的規範和之積形式。

基本信息

介紹

所有的文字的合取和所有的文字的析取是 CNF 的，因為可以被分別看作一個文字的子句的合取和一個單一子句的合取。和析取範式(DNF)中一樣，在 CNF 公式中可以包含的命題連結詞是與、或和非。非運算元只能用做文字的一部分，這意味著它只能在命題變數前出現。

例子

例如，下列所有公式都是 CNF:

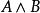合取範式定理

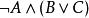合取範式定理

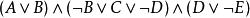合取範式定理

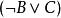合取範式定理

而下列不是:

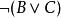合取範式定理

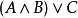合取範式定理

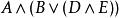合取範式定理

上述三個公式分別等價於合取範式的下列三個公式:

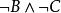合取範式定理

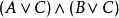合取範式定理

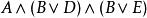合取範式定理

所有命題公式都可以轉換成 CNF 的等價公式。這種變換基於了關於邏輯等價的規則:雙重否定律、德·摩根定律和分配律。

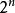合取範式定理

因為所有邏輯公式都可以轉換成合取範式的等價公式，證明經常基於所有公式都是 CNF 的假定。但是在某些情況下，這種到 CNF 的轉換可能導致公式的指數性爆漲。例如，把下述非-CNF 公式轉換成 CNF 生成有 個子句的公式:

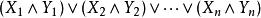合取範式定理