基本介紹
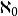 至多可數集
至多可數集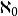 至多可數集
至多可數集自然數集N的基數記作 (讀作“阿列夫零”),若A~N,則稱A為可數集。有限集與可數集統稱為 至多可數集,即能夠與自然數集N的某一子集構成一一對應的集,亦即基數不超過 的集。至多可數個至多可數集的和集是至多可數集;有限個至多可數集的直積也是至多可數集。若無限集E不是可數集,則稱E為不可數集。
 至多可數集
至多可數集集合A為可數集若且唯若A= { },即A中的元可以用自然數來編號 。
相關定理
定理1 任一無限集E必含一個可數子集。
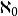 至多可數集
至多可數集上述定理說明:在無限集的基數中,最小的基數是 .
定理2 N×N是可數集。
不難知道:若A,B是可數集,則直積集A×B也是可數集.一般地,用歸納法可以證明:若每個E(k=1,2,3,...,n)是可數集,則直積集E×E×...×E也是可數集.
 至多可數集
至多可數集定理3 若每個A(n=1,2,3,...)是可數集,則並集也是可數集。
上述定理也常稱為:可數個可數集之並是可數集。
另外不難證明:若有至多可數個集作並集,且每個集合都是至多可數集,則其並集也是至多可數集。
推論4 R 中的有理數集Q是可數集,R 中的有理點集Q 是可數集。
定理5 若E為無限集,A為至多可數集,則E~E∪A。
證 不妨設E∩A=∅,由定理1,知無限集E有可數子集D.因為A為至多可數集,於是有D~A∪D。於是:
E=(E\D)∪D~(E\D)∪(D∪A)=EUA.
推論6 設E為不可數集,A是E的可數子集,則E~E\A。
證 首先易知E\A不是有限集,因為否則E=(E\A)∪A要為可數集,得矛盾.所以E\A必為無限集,而A是可數集,所以由定理5知E\A~(E\A)∪A=E 。
例題解析
例1設Γ是R 中的一族開區間,若每個開區間的端點為有理數,則Γ是至多可數集。
 至多可數集
至多可數集證對Γ中的開區間(a,b),令Q×Q中的點(a,b)與之對應,得到從Γ到Q×Q的一個單射,所以,從而可得Γ是至多可數集。
例2 設Γ是R 中的一族開區間,若其中任意兩個開區間互不相交,則Γ是至多可數集。
 至多可數集
至多可數集證 對Γ中的每個開區間I,取定I中的一個有理數作為f(I),則f:Γ→Q是一個單射,所以,從而可得Γ是至多可數集 。

