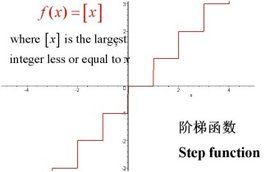
定義
不超過實數x的最大整數稱為x的整數部分，記作[x]或INT(x)。
x-[x]稱為x的小數部分，記作{x}。
（需要注意的是，對於負數，[x]並非指x小數點左邊的部分，{x}也並非指x小數點右邊的部分，例如對於負數-3.7，[-3.7]=-4，而不是-3，此時{x}=-3.7-(-4)=0.3，而不是-0.7.）
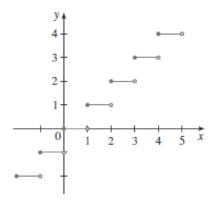取整函式圖象相關概念
【階梯曲線】
即取整函式的在定義域D=（-∞，+∞），值域Rf=Z的圖形，在x為整數值處，圖形發生跳躍，越度為1。
性質
性質1 對任意x∈R,均有x-1<[x]≤x<[x]+1.
性質2對任意x∈R,函式y={x}的值域為[0,1)
性質3 取整函式(高斯函式)是一個不減函式,即對任意x1,x2∈R,若x1≤x2,則[x1]≤[x2].
性質4若n∈Z,x∈R,則有[x+n]=n+[x],{n+x}={x}.後一式子表明y={x}是一個以1為周期的函式.
性質5 若x,y∈R,則[x]+[y]≤[x+y]≤[x]+[y]+1.
性質6若n∈N+,x∈R,則[nx]≥n[x].
性質7若n∈N+,x∈R+,則在區間[1,x]內,恰好有[x/n]個整數是n的倍數.
性質8設p為質數,n∈N+,則p在n!的質因數分解式中的冪次為
p(n!)=[n/p]+[n/p ]+….
厄米特恆等式
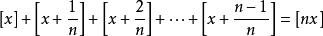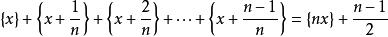取整函式
取整函式套用
取整函式與微積分有著緊密聯繫，它在科學和工程上有廣泛套用。
