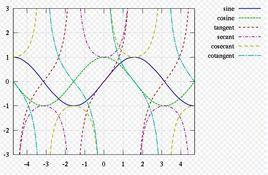
基本概念
反正割函式 反正割函式 反正割函式 反正割函式反三角函式之一.指正割函式y=sec x在區間[0，π/2)∪(π/2，π]上的反函式.記為y=arcsec x或y=secx.它表示[0，π/2)∪(π/2，π]上正割值等於x的那個惟一確定的角，即sec(arcsec x)=x，反正割函式的定義域是(-，-1]∪[1，+)，值域是[0，π/2)∪(π/2，π].由於正割函式在區間[0，π/2)∪(π/2，π]上是單調連續的，因此，反正割函式是存在且惟一確定的.引進多值函式概念後，就可以在正割函式的整個定義域(x∈R，且x≠kπ+π/2，k∈Z)上來考慮它的反函式，這時的反正割函式是多值的，記為y=Arcsec x，定義域是(-，-1]∪[1，+)，值域是y∈R，y≠kπ+π/2，k∈Z.
反正割函式 反正割函式 反正割函式 反正割函式 反正割函式 反正割函式於是，把y=arcsec x(x∈(-，-1]∪[1，+)，y∈[0，π/2)∪(π/2，π])稱為反正割函式的主值，而把y=Arcsec x=2kπ±arcsec x(x∈(-，-1]∪[1，+)，y∈R，y≠kπ+π/2，k∈Z)稱為反正割函式的通值.反正割函式在區間(-，-1]∪[1，+)上的圖象可由區間[0，π/2)∪(π/2，π]上的正割曲線作關於直線y=x的對稱變換而得到.
定義
反正割函式 反正割函式（由於反函式存在的條件為原函式單調，但y=secx ,{x|x∈R，x≠π/2+kπ,k∈Z} 在定義域內不單調）所以定義：y=secx，x∈[0，π/2)∪(π/2，π]的反函式為 反正割函式， 記作y=arcsecx,x∈(-，-1]∪[1，+) ， y∈[0，π/2)∪(π/2，π]，注意：y表示的是一個弧度制的角，自變數x是一個正割值
理解
函式其實就是一個數集A到另一個數集B的映射f，（一般A∈R，B∈R，A ∉ ∅，B∉ ∅），若且唯若f是一一映射時，它才有逆映射f-1（-1在f右上角，以下所有“f-1”均如此）。顯然f-1也是一一映射，它也有逆映射f。因而f與f-1互為逆映射。可見，函式y=f(x)與函式x=f-1(y)互為反函式。由於習慣上常用x表示自變數，y表示函式，因而在函式x=f-1(y)的表達式中，一般都還要對調字母x和y，把它改成y=f-1(x)
像與原像 ：設A，B是兩個非空集合，如果根據某個確定的對應法則f使得對A中的每一個元素a，集合B中都有唯一的一個元素b和它對應，那么這種對應叫做集合A到集合B的映射，記作f：A→B。而b叫做a(在f作用下的）的像，記作b=f(a)，a叫做（b在f作用下）的原像。顯然，原像集就是集合A，而像集與B之間有關係 f(A)⊆B
性質
取值
反正割函式 反正割函式x∈(-，-1]∪[1，+) ，y∈[0，π/2)∪(π/2，π]
最值
當x=-1時，有最 大值π， 當x=1時，有最 小值0
單調性
反正割函式 反正割函式 反正割函式 反正割函式由於正割函式y=secx 在 [0，π/2)上單調遞增，所以反正割函式y=arcsecx 在 (-，-1]上單調 遞增。同理 反正割函式y=arcsecx 在 [1，+) 上單調 遞增。即單調遞增區間：(-，-1]、[1，+) （ 注意： 絕對不能並起來 ）
對稱中心
反正割函式 反正割函式(0，π/2)，故有 arcsec(x)+arcsec(-x)=π， x∈(-，-1]∪[1，+)
漸近線
直線y=π/2
導數
y'=(x^2)√【1-（1/x^2）】 y'始終大於0。
y'=x^2√【1-（1/x^2）】 的推導詳細推導：
將其分段的答案合併即為 (x^2)√【1-（1/x^2）】
基本思想為：原函式的導數=其反函式導數的倒數，即dy/dx=1/(dx/dy)
函式圖像
由以上 y=arcsecx 的導數推導的圖中，第一行cosy=1/x，所以y=arccos(1/x)。以此作為理論依據在幾何畫
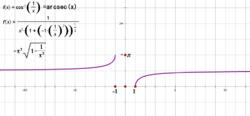y=arcsecx的圖像板中作出 y=arcsecx的圖像。
自己作圖：
我們知道這個結論：“ 函式f(x)的圖像和它的反函式的圖像關於直線y=x對稱”，
①可以先畫出函式y=secx在(－π/2，π/2)上的圖像
②用平板玻璃或透明紙畫好圖像，翻轉過來。或根據另一結論：點P(x0，y0)關於直線y=x的對稱點為（y0，x0），描出數點後即可作出圖形。
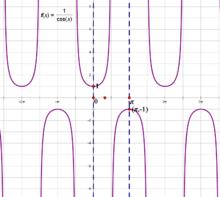y=secx=1/cosx的圖像（取右圖兩條虛線之間的部分 作反函式即可。）
