基本介紹
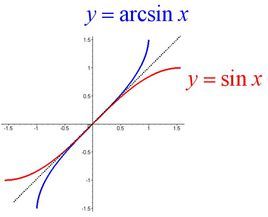
正弦函式y=sinx，x∈[-½π,½π]的反函式叫做反正弦函式，記作y=arcsinx，x∈[-1,1]。習慣上用x表示自變數，用y表示因變數(函式值)，所以反正弦函式寫成y=arcsinx的形式
請注意正弦函式y=sinx，x∈R因為在整個定義域上沒有一一對應關係，所以不存在反函式。
反正弦函式只對這樣一個函式y=sinx，x∈[-½π,½π]成立，這裡截取的是正弦函式靠近原點的一個單調區間，叫做正弦函式的主值區間。
理解函式y=arcsinx中，y表示的是一個弧度制的角，自變數x是一個正弦值，siny=x或x=siny更易理解。
性質
根據反函式的性質，易得函式y=arcsinx的
arcsinx的含義：
（1）這裡的x滿足 ；
（2） arcsinx是 （主值區）上的一個角（弧度數）；分得再細一點，即當 時， ；當 時， 。
（3）這個角（弧度數）的正弦值等於x，即sin（arcsinx）=x.
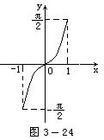
函式圖象：我們知道這個結論“函式y=f（x）的圖象和它的反函式y=f-1（x）的圖象關於直線y=x對稱”，先畫出函式y=sinx在 上的圖象，用平板玻璃或透明紙畫好圖象，翻轉過來，從圖象上我們可以得到以下兩個結論：
（1）反正弦函式y=arcsinx在區間【-1，1】上是增函式；
（2）反正弦函式y=arcsinx的圖象關於原點對稱，這說明它是奇函式，也就是arcsin（-x）=-arcsinx，x∈【-1，1】.
反正弦恆等式
sin(arcsinx)=x，x∈[-1，1](arcsinx)'=1/√(1-x^2)arcsinx=-arcsin(-x)
arcsin（sinx)=x，x屬於[-π/2，π/2]
函式圖像
我們知道這個結論函式f(x)的圖像和它的反函式的圖像關於直線y=x對稱”，先畫出函式y=sinx在[－π/2，π/2]上的圖像，用平板玻璃或透明紙畫好圖像，翻轉過來。
證明
單調性
在x，y∈[-π/2,π/2]x<y時：sinx-siny=2sin[(x-y)/2]cos[(x+y)/2]
∵2sin[(x-y)/2]∈[-π,0]<>0
cos[(x+y)/2]∈[-π,0]><0
∴sinx-siny<0,sinx<siny.
∴在-1<x<y<1時，arcsinx<arcsiny
∴是增函式
奇偶性
∵y=sinx,y=x都是奇函式，∴y=arcsinx也是奇函式套用
臨界角是最少的入射角使得全內反射發生。入射角是由折射界面的法線量度。其中n2是較低密度介質的折射率，及n1是較高密度介質的折射率。這條方程式是一條斯涅爾定律的簡單套用，當中折射角為90°。 當入射光線是準確的等於臨界角，折射光線會循折射界面的切線進行。以可見光由玻璃進入空氣（或真空）為例，臨界角約為41.5°。
