定義
原根是一種數學符號,設m是正整數,a是整數,若a模m的階等於φ(m),則稱a為模m的一個原根。(其中φ(m)表示m的歐拉函式)
假設一個數g是P的原根,那么g^i mod P的結果兩兩不同,且有 1<g<P,0<i<P,歸根到底就是g^(P-1) = 1 (mod P)若且唯若指數為P-1的時候成立.(這裡P是素數)。
簡單來說,g^i mod p ≠ g^j mod p (p為素數),其中i≠j且i, j介於1至(p-1)之間,則g為p的原根。
求原根目前的做法只能是從2開始枚舉,然後暴力判斷g^(P-1) = 1 (mod P)是否若且唯若指數為P-1的時候成立。而由於原根一般都不大,所以可以暴力得到。
性質
原根具有以下性質:
(1)可以證明,如果正整數( a, m) = 1和正整數 d 滿足a^d≡1(mod m),則 d 整除 φ( m)。因此 O r d m( a)整除φ( m)。在例子中,當 a= 3時,我們僅需要驗證 3 的 1 、2、3 和 6 次方模 7 的餘數即可。
(2)記δ = O r d m( a),則a^1,……a^(δ-1)模 m 兩兩不同餘。因此當 a是模 m的原根時,a^0,a^1,……a^(δ-1)構成模 m 的簡化剩餘系。
(3)模 m有原根的充要條件是 m= 1,2,4, p,2 p, p^n,其中 p是奇質數, n是任意正整數。
(4)對正整數( a, m) = 1,如果 a 是模 m 的原根,那么 a 是 整數模n乘法群(即加法群 Z/m Z的可逆元,也就是所有與 m 互素的正整數構成的等價類構成的乘法群) Zn的一個生成元。由於 Zn有 φ( m)個元素,而它的生成元的個數就是它的可逆元個數,即 φ(φ( m))個,因此當模 m有原根時,它有φ(φ( m))個原根。
原根存在條件
原根存在的條件有以下幾個:
定理一:設p是奇素數,則模p的原根存在;
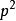 原根
原根定理二:設g是模p的原根,則g或者g+p是模的原根;
 原根
原根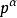 原根
原根定理三:設p是奇素數,則對任意,模的原根存在;
 原根
原根 原根
原根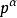 原根
原根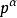 原根
原根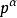 原根
原根定理四:設1,則g是模的一個原根,則g與g+中的奇數是模2的一個原根。
例子
設 m= 7,則φ(7)等於6。
設 a= 2,由於2^3=8≡1(mod 7),2^6=64≡1(mod7),2^3≡2^6(mod7),所以 2 不是模 7 的一個原根。設 a= 3,由於3^1≡3(mod 7),3^2≡2(mod 7),3^3≡6(mod 7),3^4≡4(mod 7),3^5≡5(mod 7),3^6≡1(mod 7),所以 3 是模 7 的一個原根。
補充一點,根據原根的性質1,只需要驗證3^1,3^2,3^3,3^6即可,這樣可以簡化運算。

