雙原子分子電子態
 原子結構(含電子,質子,中子)-模型圖
原子結構(含電子,質子,中子)-模型圖正文
按照雙原子分子電子的總角動量量子數和波函式的空間對稱性來分類的分子狀態。這種狀態在一定程度上可以用雙原子分子的電子組態來推斷,但具體光譜項一般還需要進一步用電子光譜來決定。分類和標記 軌道角動量 分子中兩核的聯線稱為分子軸,兩核產生的電場是軸對稱的。電子在此軸對稱的電場中運動時,其總軌道角動量L繞分子軸進動,它在分子軸上的分量取值為
 ML絕對值不同的電子系統有不同的能量,因此可用ML的絕對值Λ標記雙原子分子的電子態:
ML絕對值不同的電子系統有不同的能量,因此可用ML的絕對值Λ標記雙原子分子的電子態: 
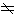 0的態是雙重簡併的,也就是
0的態是雙重簡併的,也就是 態簡併,稱為Λ雙重態。
態簡併,稱為Λ雙重態。 自鏇角動量 雙原子分子電子光譜帶具有多重結構,它來源於電子的自鏇與磁場相互作用。在雙原子分子中,各電子的自鏇合成總自鏇角動量S),自鏇量子數S取整數或半整數,由電子數為偶數或奇數而定。Λ
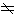 0時,電子的軌道運動形成一軸向內磁場,並引起S) 繞分子軸進動,S)在分子軸方向的分量是MS(h/2π)。將量子數MS記為 ч,其允許值為
0時,電子的軌道運動形成一軸向內磁場,並引起S) 繞分子軸進動,S)在分子軸方向的分量是MS(h/2π)。將量子數MS記為 ч,其允許值為 ч=S,S-1,S-2,…,-S。
對於一定的S值,有2S+1個不同的∑值。∑不同時分子能量稍有不同,電子光譜項因此分裂成2S+1個成分。Λ=0時分子沒有軸向內磁場,若不考慮它的轉動,光譜項不分裂。但不論Λ 是否為零,總把2S+1個值稱為電子態(以及相應的光譜項)的多重性。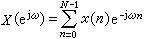 、的態分別稱為單態、雙重態、三重態等等。電子態的多重性標記在分子電子態符號的左上角,例如,
、的態分別稱為單態、雙重態、三重態等等。電子態的多重性標記在分子電子態符號的左上角,例如,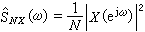 等。
等。 總角動量 總角動量是總軌道角動量、總自鏇的矢量和。當Λ=0時,電子的總角動量就是總自鏇,此時總角動量的量子數Ω =S。當Λ
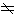 0時
0時 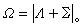
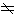 0的態就沒有必要作這樣的區分。當考慮分子的轉動時,這種雙重簡併解除。
0的態就沒有必要作這樣的區分。當考慮分子的轉動時,這種雙重簡併解除。 對於等電荷核分子,波函式在中心反演 (r→-r)作用下,或者不變或者改變符號,前者稱為偶態,後者稱為奇態,在電子態符號的右下角分別用g和u表示,例如
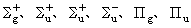 等等。
等等。 分子軌道的單電子態 量子數λ 雙原子分子中各電子在兩核的電場和其他電子的平均場中運動,由於原子核的質量比電子的大得多,可將快的電子運動和慢的原子核運動分開處理,在計算電子運動時,可近似地認為分子中原子核保持某種固定構形,則其哈密頓算符是常數。取消原子核的動能算符而算得以核構形中各原子核坐標為參數的電子波函式,這就是玻恩-奧本海默近似。在初步近似中,可用單電子波函式來描述各電子的狀態。電子的軌道角動量在分子軸方向分量的量子數ml被嚴格確定, ml=0、±1、±2、…。常用λ標記ml的絕對值 (λ=│ml│)。電子軌道角動量在分子軸上的分量的絕對值為λ(h/2π),λ=0,1,2,3,…,相應的電子分別稱為σ、π、δ、嗞、…電子, 所有π、δ、嗞等λ
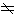 0的單電子態都是雙重簡併的。
0的單電子態都是雙重簡併的。 分子軌道和原子軌道的相關 對於不等電荷核分子,當A、B兩種核的距離趨於零時,就得到聯合原子的極端情況,其核電荷數為ZA+ZB,此時電子態由原子的量子數n、l和λ=│ml│確定,λ=0,1,…,l。記為1sσ, 2sσ,2pσ, 2pπ, 3sσ, 3pσ, 3pπ,3dσ,3dπ和 3dσ等。當兩核逐漸分開時,由於軸對稱電場的作用,λ 不同的能級簡併逐漸解除,n和l也逐漸失去了作用(但電子態的數目並不因此改變)。圖1的左邊表示聯合原子軌道和分子軌道的這種相關情況。另一極端情況是假定兩核分開無限遠,得到分離原子近似。當A、B兩原子靠近時,由於軸對稱電場的作用,比較靠近並且λ值相同的原子軌道互相聯合組成分子軌道。圖1右邊表示分子軌道和分離原子軌道的相關。從相關圖可見,分離原子和聯合原子的n、l值通常不一樣,但它們之間有一定的關聯。用聯合原子的符號(1sσ 等)和用分離原子的符號(σ1sA等)來表示分子軌道是等價的。
 雙原子分子電子態
雙原子分子電子態 雙原子分子電子態
雙原子分子電子態雙原子分子的電子組態 基態電子組態 根據泡利不相容原理,對一定的n和l的量子態只能有兩個σ 電子
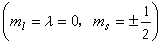 ,而對於π、δ、嗞等λ
,而對於π、δ、嗞等λ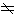 0的量子態只能各有四個電子
0的量子態只能各有四個電子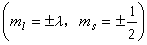 。基態的分子能量最低,電子首先填充能量較低的能級(參照圖1、2的順序)。不同的分子能級的順序可能不一樣。
。基態的分子能量最低,電子首先填充能量較低的能級(參照圖1、2的順序)。不同的分子能級的順序可能不一樣。 從電子組態推斷電子態 當已知電子組態時,可以根據一定的耦合模型來推斷分子的電子態。
許多情形可採用羅素-桑德斯耦合模型(見LS 耦合)。因為滿充支殼層Λ和S都為零,所以確定電子態時只需考慮未滿充的支殼層。
不等電荷核分子的電子態偶、奇性取決於電子組態中奇態電子的數目。若奇態電子數為偶數時,分子的電子態為偶;奇態電子數為奇數時分子的電子態為奇。
以O2分子為例, 它的基態電子組態為(σgls)2(σuls)2(σg2s)2(σu2s)2(σg2p)2(πu2p)4(πg2p)2。其中未滿充殼層是 (πg2p)2。兩個 πg電子組成 Λ=2或0,S=1或0。其中Λ=2,S=1的態違反泡利不相容原理,因此只能組成
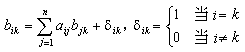 三個電子態,其中
三個電子態,其中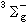 是基態。
是基態。