表述
卡諾定理是卡諾1824年提出來的,其表述如下:
⑴在相同的高溫熱源和相同的低溫熱源之間工作的一切可逆熱機,其效率都相等,與工作物質無關,與可逆循環的種類也無關。
⑵在相同的高溫熱源和相同的低溫熱源之間工作的一切不可逆熱機,其效率都小於可逆熱機的效率。
卡諾介紹
原理解釋
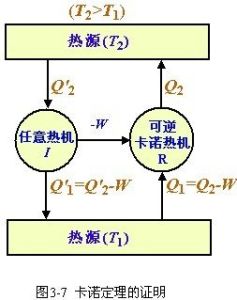
設在兩個熱源之間,有可逆機R(即卡諾機)和任意的熱機I在工作(圖2.2)。調節兩個熱機使所作的功相等。可逆機及從高溫熱源吸熱Ql,作功W,放熱(Ql-W)到低溫熱源,其熱機效率為 ηk = W/QI(圖中所示是可逆機R倒開的結果)。
另一任意熱機I,從高溫熱源吸熱Q1’,作功W,放熱(Q1’-W)到低溫熱源,其效率為
ηI = W/Q1’
先假設熱機I的效率大於可逆機R(這個假設是否合理,要從根據這個假定所得的結論是否合理來檢驗)。即
ηI > ηk,
因此得
Ql > Q1’
今若以熱機I帶動卡諾可逆機R,使R逆向轉動,卡諾機成為制冷機,所需的功W由熱機I供給,如圖2.2所示:及從低溫熱源吸熱(Ql-W),並放熱Ql到高溫熱源。整個複合機循環一周后,在兩機中工作的物質均恢復原態,最後除熱源有熱量交換外,無其它變化。
從低溫熱源吸熱:
(Ql - W) - (Q1’ - W) = Ql-Q1’ > 0
高溫熱源得到的熱:
Ql-Q1’
淨的結果是熱從低溫傳到高溫而沒有發生其它的變化。這違反熱力學第二定律的克勞修斯說法。所以最初的假設ηI>;ηk不能成立。因此應有
ηI≤ηk (2.1)
這就證明了卡諾定理。
根據卡諾定理,可以得到如下的推論:“所有工作於同溫熱源與同溫冷源間的可逆機,其熱機效率都相等”。可證明如下:假設兩個可逆機Rl和R2,在同溫熱源與同溫冷源間工作。若以Rl帶動Rl,使其逆轉,則由式(2.1)知
ηR1≤ηR2 (2.2)
反之,若以R2帶動Rl,使其逆轉,則有
ηR1≥ηR2 (2.3)
因此,若要同時滿足式(2.2)和(2.3),則應有
ηR1=ηR2 (2.4)
由此得知,不論參與卡諾循環的工作物質是什麼,只要是可逆機,在兩個溫度相同的低溫熱源和高溫熱源之間工作時,熱機效率都相等,即任意熱機I是可逆機時,式(2.1)用等號,I是不可逆機時用不等號。在上述證明中,並不涉及工作物質的本性,因而與工作物質的本性無關。在明確了ηR與工作物質的本性無關後,我們就可以引用理想氣體卡諾循環的結果了。
意義
卡諾定理雖然討論的是可逆機與不可逆機的熱機效率問題,但它具有非常重大的意義。它在公式中引入了一個不等號。前已述及所有的不可逆過程是互相關聯的。由一個過程的不可逆性可以推斷到另一個過程的不可逆性,因而對所有的不可逆過程就可以找到一個共同的判別準則。由於熱功交換的不可逆,而在公式中所引入的不等號,這對於其它過程(包括化學過程)同樣可以使用。就是這個不等號解決了化學反應的方向問題。同時,卡諾定理在原則上也解決了熱機效率的極限值問題。
卡諾循環的構成
熱力學第二定律指出,熱機的熱效率不可能達到100%。那么,在一定條件下,熱機的熱效率最大能達到多少?它又與哪些因素有關?法國工程師卡諾(S. Carnot)在深入考察了蒸汽機工作的基礎上,於1824年提出了一種理想的熱機工作循環—卡諾循環。
設一熱機中有一定量的工質,工作在溫度分別為T1和T2的兩恆溫熱源間。卡諾循環由兩個可逆的定溫過程和兩個可逆的絕熱過程(定熵)組成
四個過程的順序如下:
定溫膨脹過程a-b:工質在定溫T1下,從高溫熱源吸熱Q1並作膨脹功Wo。
定熵膨脹過程b-c:工質在可逆絕熱條件下膨脹,溫度由T1降到T2。
定溫壓縮過程c-d:工質在定溫T2下被壓縮,過程中將熱量Q2傳給低溫熱源。
定熵壓縮過程d-a;工質在可逆絕熱條件下被壓縮,溫度由T2升高至T1,過程終了時,工質的狀態回復到循環開始的狀態a。
逆卡諾循環
如果沿卡諾循環相反的方向進行,就形成卡諾製冷循環和卡諾熱泵循環。
對於卡諾製冷循環,工質可逆定溫從溫度為T2冷庫吸熱,被可逆絕熱壓縮後,可逆定溫向溫度為T1環境介質放熱,最後可逆絕熱膨脹,進入冷庫,完成循環。其製冷係數為Q2/W或T2/T1-T2。
對於卡諾熱泵循環,工質可逆定溫從低溫熱源T2,如環境介質吸熱,被可逆絕熱壓縮後,可逆定溫向高溫熱源T1,如建築物室內放熱,最後可逆絕熱膨脹,完成循環。其供暖係數或熱泵工作性能係數
應當指出,逆卡諾循環雖然實際上不能實現,但卻為提高制冷機和熱泵的完善程度指明了方向,仍具有重要的理論意義。
圖 4-2 卡諾定理證明用圖
對於第一定理的證明
下面用反證法對第一定理進行證明:假設在溫度為T1的高溫熱源與溫度為T2的低溫熱源間工作有兩個任意的可逆熱機R1和R2,如圖4-2(a)所示,其熱效率分別為和。假如,則當兩個熱機從高溫熱源吸取的熱量都為Q1時,根據熱效率的定義可知, ,。這時可讓熱機R1按正向循環工作,用輸出功中的一部分 帶動熱機R2逆向循環工作,如圖4-2(b)所示。聯合運行的結果是每一循環從低溫熱源吸收熱量,對外作功,高溫熱源沒有任何變化,相當於一台單一熱源的第二類永動機。這顯然違背了熱力學第二定律,因此是不可能的。同樣可以證明,也是不可能的。於是只有一種可能性,即。由於上述證明沒有限定工質的性質,所以結論對使用任何工質的可逆熱機都適用。定理二可以同樣採用反證法證明,思路與定理一的證明相同。
卡諾定理(數學)
概述
三角形外心到各邊距離之和等於外接圓半徑與內接圓半徑之和,這一定理稱為卡諾定理,在推斷李代數等領域中的三角形性質中有重要作用。
引理
在外接圓半徑為R,內接圓半徑為r的三角形ABC中,r和R有如下關係:
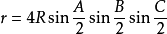 卡諾定理
卡諾定理證明
假設ABC為外心為D的銳角三角形,外心到AB、BC、AC的距離分別為DG、DH、DF,則在三角形HDB中,由外心性質可得
DB=R
角HDB=角A
由此,DH的表達式為
DH=RcosA
同理DG=RcosC、DF=RcosB。
因此,
 卡諾定理
卡諾定理根據引理,得證
DG+DH+DF=R+r
當ABC為鈍角三角形,且角B大於90°時,則有
DH=RcosA
DF=Rcos(π-B)=-RcosB
DG=RcosC
所以DG+DH-DF=R(cosA+cosB+cosC)=R+r,結論相同,卡諾定理得證。
二
平面幾何中的卡諾定理
定理
線段AB,CD垂直的充要條件為
AC^2-BC^2=AD^2-BD^2
證明
由勾股定理及其逆定理不難得證
套用
解決與圓有關的證明垂直的問題的一種計算方式