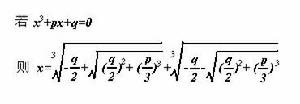 卡當公式
卡當公式三次方程解法被稱為“卡爾達諾公式”或“卡當公式”也稱為“卡爾丹公式”流傳開來.卡爾達諾公布的解法可簡述如下:
方程
x^3+px=q(p,q為正數). (1)
卡爾達諾以方程x3+6x=20為例說明這一方法,他得到的解是x=過同樣的程式得到他還求出x^3+px+q=0和x^3+q=px(p,q為正數)的公式解,就是說他已經能解任何形式的三次方程了.毫無疑問,這裡包含了塔爾塔利亞的工作.但需要說明的是,他們像當時其他數學家一樣,解方程只求正根,所以解法還是不完善的.管會受到多大的良心的責備”,把這兩個根相乘,會得25-(-15)=40.於是他寫道:“算術就是這樣神秘地搞下去的,它的目標,正如常言所說,是又精緻又不中用的.”他既承認負數有平方根,又懷疑它的合法性,因此稱它為“詭變數”.但不管怎樣,虛數畢竟在卡爾達諾那裡誕生了.他還進一步指出,方程(指實係數方程)的虛根是成對出現的.
三次方程成功地解出之後,卡爾達諾的學生費拉里(L.Ferrari,1522—1565)受到啟發,很快解出了四次方程,解法也發表在卡爾達諾《大術》中.下面用現代符號表出.
設方程為x^4+bx^3+cx^2+dx+e=0. (4)
移項,得x^4+bx^3=-cx^2-dx-e,
右邊為x的二次三項式,若判別式為0,則可配成x的完全平方.解這個三次方程,設它的一個根為y0,代入(5),由於兩邊都是x的完全平方形式,取平方根,即得
解這兩個關於x的二次方程,便可得到(4)的四個根.顯然,若把(6)的其他根代入(5),會得出不同的方程,但結果是一樣的.
在卡爾達諾之後,韋達對三次方程和四次方程解法作了進一步改進.1591年發表的《分析術引論》(Inartemanalyticemisagoge)中,他是這樣解三次方程的:
對於 x3+bx^2+cx+d=0,
結果得到簡約三次方程
y^3+py+q=0 他和卡爾達諾一樣,只考慮方程的正根.
韋達不僅研究方程解法,還努力尋找方程的根與係數的關係,在《論方程的識別與修正》(Deaequationumrecog-nitoneetemendatjone,寫於1591年,出版於1615年)中,他提出了四個定理,後人為了紀念這位大數學家,稱之為韋達定理.二次方程的韋達定理是我們經常使用的,就
對方程理論作出重要貢獻的另一位數學家是笛卡兒.他承認方程的負根,並研究了多項式方程的正根和負根個數的規律,得到著名的笛卡兒符號法則:多項式方程f(x)=0的正根個數等於方程係數的變號次數,或比此數少一正偶數;負根個數等於f(-x)的係數的變號次數,或少於此數一個正偶數.在這裡,m重根是看作m個根的.實際上,正根個數和負根個數都可表成n-2p的形式,其中n是f(x)或f(-x)的係數變號次數,p為0,1,2…,p的取值要使n-2p非負.笛卡兒還研究了方程的根的個數同方程次數的關係,認為n次方程至多有n個根.在討論三次方程時,他得到如下結論:若一有理係數三次方程有一個有理根,則此方程可表為有理係數因子的乘積.他的另一項重要成果是現今所謂因子定理:f(x)能為(x-a)整除(a>0),若且唯若a是f(x)=0的一個根,所有這些成就都是在笛卡兒《方法論》(DiscoursdelaMéthod,1637)的附錄《幾何》(LaGéometrie)中出現的.
除了方程以外,二項式定理的發現也在代數史上占有一席之地.實際上,指數為正整數的二項式定理(即(a+b)n在n為正整數時的展開式)曾被不同民族多次獨立發現.11世紀的中國人賈憲和15世紀的阿拉伯數學家卡西(al-Kāshī)各自得到如下形式的三角形
這個三角形特點是,左右兩行的數都是1,中間每個數為肩上兩數之和.
在歐洲,德國數學家阿皮安努斯(P.Apianus,1495—1552)最早給出這個三角形(1527年),1544年左右,施蒂費爾引入“二項式係數”這個名稱,並指出怎樣從(1+a)n-1來計算(1+a)n.1653年,帕斯卡寫成《算術三角形》(Traitédutrianglearithmétique)一書,從上述三角形出發,詳細討論了二項展開式的係數.該書於1665年出版後,影響很大.由於帕斯卡在數學界的威望,人們習慣地稱此三角形為帕斯卡三角形.實際上,他的功績主要是通過組合公式給出了二項式係數,即牛頓(T.Newton,1643—1727)進一步認識到,這個公式不僅適用於指數為正整數的二項展開式,而且當指數為分數或負數時,同樣適用.他把二項式定理推廣到分指數和負指數的情形,指出這三種形式的二項展開式第1項都是1,後面各項係數及字母指數也具有相同的變化規律:設n,m為正整數,則三次方程解法被稱為“卡爾達諾公式”或“卡當公式”、“卡爾丹公式”流傳開來.卡爾達諾公布的解法可簡述如下:
方程
x^3+px=q(p,q為正數). (1)
卡爾達諾以方程x^3+6x=20為例說明這一方法,他得到的解是x=過同樣的程式得到他還求出x^3+px+q=0和x^3+q=px(p,q為正數)的公式解,就是說他已經能解任何形式的三次方程了.毫無疑問,這裡包含了塔爾塔利亞的工作.但需要說明的是,他們像當時其他數學家一樣,解方程只求正根,所以解法還是不完善的.管會受到多大的良心的責備”,把這兩個根相乘,會得25-(-15)=40.於是他寫道:“算術就是這樣神秘地搞下去的,它的目標,正如常言所說,是又精緻又不中用的.”他既承認負數有平方根,又懷疑它的合法性,因此稱它為“詭變數”.但不管怎樣,虛數畢竟在卡爾達諾那裡誕生了.他還進一步指出,方程(指實係數方程)的虛根是成對出現的.
三次方程成功地解出之後,卡爾達諾的學生費拉里(L.Ferrari,1522—1565)受到啟發,很快解出了四次方程,解法也發表在卡爾達諾《大術》中.下面用現代符號表出.
設方程為x^4+bx^3+cx^2+dx+e=0. (4)
移項,得x^4+bx^3=-cx^2-dx-e,
右邊為x的二次三項式,若判別式為0,則可配成x的完全平方.解這個三次方程,設它的一個根為y0,代入(5),由於兩邊都是x的完全平方形式,取平方根,即得
解這兩個關於x的二次方程,便可得到(4)的四個根.顯然,若把(6)的其他根代入(5),會得出不同的方程,但結果是一樣的.
在卡爾達諾之後,韋達對三次方程和四次方程解法作了進一步改進.1591年發表的《分析術引論》(Inartemanalyticemisagoge)中,他是這樣解三次方程的:
對於 x^3+bx^2+cx+d=0,
結果得到簡約三次方程
y^3+py+q=0 他和卡爾達諾一樣,只考慮方程的正根.
韋達不僅研究方程解法,還努力尋找方程的根與係數的關係,在《論方程的識別與修正》(Deaequationumrecog-nitoneetemendatjone,寫於1591年,出版於1615年)中,他提出了四個定理,後人為了紀念這位大數學家,稱之為韋達定理.二次方程的韋達定理是我們經常使用的,就
對方程理論作出重要貢獻的另一位數學家是笛卡兒.他承認方程的負根,並研究了多項式方程的正根和負根個數的規律,得到著名的笛卡兒符號法則:多項式方程f(x)=0的正根個數等於方程係數的變號次數,或比此數少一正偶數;負根個數等於f(-x)的係數的變號次數,或少於此數一個正偶數.在這裡,m重根是看作m個根的.實際上,正根個數和負根個數都可表成n-2p的形式,其中n是f(x)或f(-x)的係數變號次數,p為0,1,2…,p的取值要使n-2p非負.笛卡兒還研究了方程的根的個數同方程次數的關係,認為n次方程至多有n個根.在討論三次方程時,他得到如下結論:若一有理係數三次方程有一個有理根,則此方程可表為有理係數因子的乘積.他的另一項重要成果是現今所謂因子定理:f(x)能為(x-a)整除(a>0),若且唯若a是f(x)=0的一個根,所有這些成就都是在笛卡兒《方法論》(DiscoursdelaMéthod,1637)的附錄《幾何》(LaGéometrie)中出現的.
除了方程以外,二項式定理的發現也在代數史上占有一席之地.實際上,指數為正整數的二項式定理(即(a+b)n在n為正整數時的展開式)曾被不同民族多次獨立發現.11世紀的中國人賈憲和15世紀的阿拉伯數學家卡西(al-Kāshī)各自得到如下形式的三角形
這個三角形特點是,左右兩行的數都是1,中間每個數為肩上兩數之和.
在歐洲,德國數學家阿皮安努斯(P.Apianus,1495—1552)最早給出這個三角形(1527年),1544年左右,施蒂費爾引入“二項式係數”這個名稱,並指出怎樣從(1+a)n-1來計算(1+a)n.1653年,帕斯卡寫成《算術三角形》(Traitédutrianglearithmétique)一書,從上述三角形出發,詳細討論了二項展開式的係數.該書於1665年出版後,影響很大.由於帕斯卡在數學界的威望,人們習慣地稱此三角形為帕斯卡三角形.實際上,他的功績主要是通過組合公式給出了二項式係數,即牛頓(T.Newton,1643—1727)進一步認識到,這個公式不僅適用於指數為正整數的二項展開式,而且當指數為分數或負數時,同樣適用.他把二項式定理推廣到分指數和負指數的情形,指出這三種形式的二項展開式第1項都是1,後面各項係數及字母指數也具有相同的變化規律:設n,m為正整數“卡當公式”的一般推導
缺項的一元三次方程的一般解法,最早為義大利數學家費羅發現。後來當時的另一位著名的數學家塔爾塔利亞也在與費羅的學生菲奧爾競賽中發現這一方法,並再米蘭的卡爾達諾一再懇求下,塔爾塔利亞通過詩的形式將解法告知了卡爾達諾。卡爾達諾鑒於這一發現對當時數學的發展重要意義,最終背棄了對塔爾塔利亞許下的保守解法的誓言,於1545年發表於自己的著作《大術》之中。儘管圍繞一元三次方程解法中還存在著一些道德觀上的爭論,但我們不能否認卡爾達諾的貢獻。卡爾達諾在大術不僅給予了公式解,還進行了幾何意義上的證明。卡爾達諾幾何意義上的證明是利用不斷逼近方體的體積來實現的。因此,在此處筆者將利用公式缺項處理,對該公式做一推導。
由一元三次方程的完整式X3+a1X2+a2X+a3=0 (1)
和缺項式X3+pX+q=0 (2)可知,
欲將式 (1)轉換為式 (2),
需令y=X-a1/3代入式 (1),
得(X-a1/3)3+a1(X-a1/3)2+…=0,
化簡後,其中含X2的項已經抵消,這樣就將問題化為了式(2)的形式了。
令X=u+v,於是將其代入式(2)中,
則(u+v)3+p(u+v)+q=0 (3),
化簡易得(u3+v3)+q+(u+v)(3uv+p)=0(4)
由於u、v是兩個變數,而該處僅置一個方程,
為通過u、v確定X則需設(u3+v3)+q=0(5)和(u+v)(3uv+p)=0(6),
由此得u3+v3=-q,u3v3=-P3/27,
依此做一元二次方程Z2+qZ-p3/27=0,
則得u3=-q/2+(q2/4+p3/27)1/2,v3=-q/2-(q2/4+p3/27)1/2,
則方程解應為X=[-q/2+(q2/4+p3/27)1/2]1/3+[-q/2-(q2/4+p3/27)1/2]1/3,
因為方程根式還有虛數根存在,化簡篩選既可得出三個根解。
由方程式判別式D確定,D<0時,方程有三根;當D=0時,X1=2(-q/2)1/3,X2=X3=(q/2)1/3;當D>0,只有一實根,其餘兩根為共軛複數根。
