簡介
卡方分布 卡方分布分布在數理統計中具有重要意義。 分布是由阿貝(Abbe)於1863年首先提出的，後來由海爾墨特(Hermert)和現代統計學的奠基人之一的卡·皮爾遜(C K．Pearson)分別於1875年和1900年推導出來，是統計學中的一個非常有用的著名分布。
定義
卡方分布
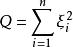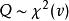卡方分布 卡方分布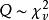
卡方分布 卡方分布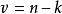
卡方分布
卡方分布
卡方分布
卡方分布若n個相互獨立的隨機變數ξ₁、ξ₂、……、ξn ，均服從標準常態分配（也稱獨立同分布於標準常態分配），則這n個服從標準常態分配的隨機變數的平方和 構成一新的隨機變數，其分布規律稱為 分布（chi-square distribution），其中參數 稱為自由度，正如常態分配中均數或方差不同就是另一個常態分配一樣，自由度不同就是另一個 分布。記為 或者 （其中 ， 為限制條件數）。
卡方分布 卡方分布卡方分布是由常態分配構造而成的一個新的分布，當自由度 很大時， 分布近似為常態分配。
卡方分布對於任意正整數 x， 自由度為 的 卡方分布是一個隨機變數 X的機率分布。
性質
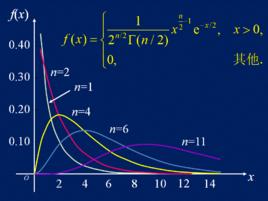
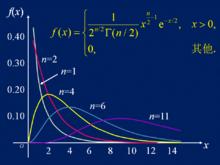
卡方分布 卡方分布 卡方分布1) 分布在第一象限內，卡方值都是正值，呈正偏態（右偏態），隨著參數 的增大， 分布趨近於常態分配；卡方分布密度曲線下的面積都是1.
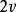卡方分布 卡方分布 卡方分布
卡方分布2) 分布的均值與方差可以看出，隨著自由度 的增大，χ2分布向正無窮方向延伸（因為均值 越來越大），分布曲線也越來越低闊（因為方差 越來越大）。
3）不同的自由度決定不同的卡方分布，自由度越小，分布越偏斜。
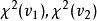卡方分布
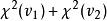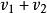卡方分布 卡方分布
卡方分布4) 若 互相獨立，則： 服從 分布，自由度為 ；
卡方分布 卡方分布 卡方分布 卡方分布5)分布的均數為自由度，記為 E() =。
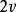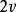卡方分布 卡方分布 卡方分布 卡方分布6) 分布的方差為2倍的自由度( )，記為 D( ) = 。
機率表
卡方分布臨界值表 卡方分布 卡方分布 卡方分布 卡方分布 卡方分布 卡方分布 卡方分布 卡方分布 卡方分布 卡方分布分布不象常態分配那樣將所有常態分配的查表都轉化為標準常態分配去查，在 分布中得對每個分布編制相應的機率值，這通過 分布表中列出不同的自由度來表示，在 分布表中還需要如標準常態分配表中給出不同 P 值一樣，列出機率值，只不過這裡的機率值是 值以上 分布曲線以下的機率。由於 分布機率表中要列出很多 分布的機率值，所以 分布中所給出的 P 值就不象標準常態分配中那樣給出了400個不同的 P 值，而只給出了有代表性的13個值，因此 分布機率表的精度就更差，不過給出了常用的幾個值，足夠在實際中使用了。
卡方分布 卡方分布 卡方分布查 分布機率表時，按自由度及相應的機率去找到對應的 值。如上圖所示的單側機率 0.05(7)=14.1的查表方法就是，在第一列找到自由度7這一行，在第一行中找到機率0.05這一列，行列的交叉處即是14.1。
卡方分布 卡方分布表中所給值直接只能查單側機率值，可以變化一下來查雙側機率值。例如，要在自由度為7的卡方分布中，得到雙側機率為0.05所對應的上下端點可以這樣來考慮：雙側機率指的是在上端和下端各劃出機率相等的一部分，兩機率之和為給定的機率值，這裡是0.05，因此實際上上端點以上的機率為0.05/2=0.025，用機率0.025查表得上端點的值為16，記為 0.05/2(7)=16。下端點以下的機率也為0.025，因此可以用0.975查得下端點為1.69，記為 1-0.05/2(7)=1.69。
卡方分布 卡方分布 卡方分布 卡方分布當然也可以按自由度及 值去查對應的機率值，不過這往往只能得到一個大概的結果，因為 分布機率表的精度有限，只給了 13 個不同的機率值進行查表。例如，要在自由度為 18 的 分布查找 =30 對應的機率，則先在第一列找到自由度 18，然後看這一行可以發現與 30 接近的有28.9與31.5，它們所在的列是0.05與0.025，所以要查的機率值應於介於0.05與0.025之間，當然這是單側機率值，它們的雙側機率值界於0.1與0.05之間。如果要更精確一些可以採用插值的方法得到，這在常態分配的查表中有介紹。
卡方分布為什麼從正態總體中抽取出的樣本的方差服從 分布
卡方分布 卡方分布 卡方分布在抽樣分布理論一節里講到，從正態總體進行一次抽樣就相當於獨立同分布的 n 個正態隨機變數ξ1，ξ2，…，ξn的一次取值，將 n 個隨機變數針對總體均值與方差進行標準化得(i=1,…,n)，顯然每個都是服從標準常態分配的，因此按照 分布的定義，應該服從參數為 的 分布。
卡方分布 卡方分布 卡方分布如果將總體中的方差σ 用樣本方差 s 代替，它是否也服從 分布呢？理論上可以證明，它是服從 分布的，但是參數 不是 n 而是 n-1 了，究其原因在於它是 n-1 個獨立同分布於標準常態分配的隨機變數的平方和
我們常常把一個式子中獨立變數的個數稱為這個式子的“自由度”，確定一個式子自由度的方法是：若式子包含有 n 個變數，其中k 個被限制的樣本統計量，則這個表達式的自由度為 n-k。比如中包含ξ1，ξ2，…，ξn這 n 個變數，其中ξ1-ξn-1相互獨立，ξn為其餘變數的平均值，因此自由度為 n-1。
