定義
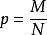超幾何分布產品抽樣檢查中經常遇到一類實際問題，假定在N件產品中有M件不合格品，即不合格率。
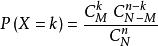超幾何分布在產品中隨機抽n件做檢查，發現k件不合格品的機率為,k=0,1,2...min{n,M}。
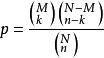超幾何分布亦可寫作（與上式不同的是M可為任意實數，而C表示的組合數M為非負整數）
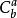超幾何分布為古典概型的組合形式，a為下限，b為上限，此時我們稱隨機變數X服從超幾何分布（hypergeometric distribution）。
需要注意的是：
（1）超幾何分布的模型是不放回抽樣。
（2）超幾何分布中的參數是M,N,n，上述超幾何分布記作X~H(n,M,N)。
套用
示例
已經知道某個事件的發生機率，判斷從中取出一個小樣本，該事件以某一個機率出現的機率問題。
例：在一個口袋中裝有30個球，其中有10個紅球，其餘為白球，這些球除顏色外完全相同。遊戲者一次從中摸出5個球。摸到至少4個紅球就中一等獎，那么獲一等獎的機率是多少？
解：由題意可見此問題歸結為超幾何分布模型。
其中N = 30. D = 10. n = 5.
P（一等獎） = P(X=4） + P(X=5）
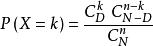超幾何分布由公式 ,k=0,1,2,...得：
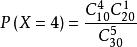超幾何分布
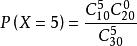超幾何分布P（一等獎） = 106/3393
期望
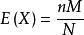超幾何分布對X~H(n,M,N) , .
證明：
引理一：∑{C(x,a)*C(d-x,b),x=0..min{a,d}}=C(d,a+b），考察（1+x)^a*（1+x)^b中x^d的係數即得。（另：還可以由超幾何分布1=∑P(X=K),k=0,1,2....n得）
引理二：k*C(k,n)=n*C(k-1,n-1），易得。
正式證明：
EX=∑{k*C(k,M)*C(n-k,N-M)/C(n,N),k=0..min{M,n}}
=1/C(n,N)*∑{M*C(k-1,M-1）*C(n-k,N-M),k=1..min{M,n}}
//（提取公因式，同時用引理二變形，注意k的取值改變）
=M/C(n,N)*∑{C(k-1,M-1）*C(n-k,N-M),k=1..min{M,n}} （提取，整理出引理一的前提）
=M*C(n-1,N-1）/C(n,N) （利用引理一）
=Mn/N （化簡即得）
方差
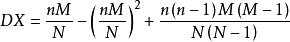超幾何分布對X~H(n,M,N) , .
證明：
DX=E(X^2）-(EX)^2 （此公式利用定義式簡單展開即得）
=∑{k^2*C(k,M)*C(n-k,N-M)/C(n,N),k=0..min{M,n}}-(Mn/N)^2
=1/C(n,N)*∑{M*k*C(k-1,M-1）*C(n-k,N-M),k=1..min{M,n}}-(Mn/N)^2（提取，變形）
=M/C(n,N)*∑{(k-1）*C(k-1,M-1）*C(n-k,N-M)+C(k-1,M-1）*C(n-k,N-M),k=1..min{M,n}}-(Mn/N)^2
（拆項，變形）
=M/C(n,N)*∑{(M-1）*C(k-2,M-2）*C(n-k,N-M),k=2..min{M,n}}+M/C(n,N)*∑{C(k-1,M-1）*C(n-k,N-M),k=1..min{M,n}}-(Mn/N)^2 （拆開∑，就是分組求和）
=M(M-1）*C(n-2,N-2）/C(n,N)+Mn/N-(Mn/N)^2
=nM(N-M)(N-n)/[(N^2）（N-1）] （化簡即得）
超幾何分布和二項分布的聯繫
超幾何分布
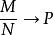超幾何分布（1）在超幾何分布中，當 時， (二項分布中的p）。
超幾何分布（2）當 時，超幾何分布的數學期望
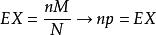超幾何分布
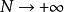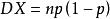超幾何分布
超幾何分布（3）當時，超幾何分布的方差（二項分布的方差）。
超幾何分布（4）當時，超幾何分布近似為二項分布。
函式代碼
超幾何分布計算函式
function HYPGEOMDIST(kkk,n,MM,NN)
for k=kkk to n
AA=1
BBA=1
BBB=1
lll=n
for i= 0 to k-1
BBA=BBA*(MM-i)/(NN-i)
next
for j= k to n
BBB=BBB*(NN-MM-j+k)/(NN-j)
next
BBs=BBB*BBA
if lll-k>k then
x=K
Else x=lll-k
end if
for i=1 to x
lll=lll-1
next
HYPGEOMDIST=HYPGEOMDIST+BBS
next
end function
response.write HYPGEOMDIST（200,2200,1000,17000)
%>
