定義
概述
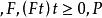 半鞅
半鞅一個定義在帶域流的機率空間(Ω)的實值隨機過程 X被稱為半鞅,若 X有如下分解:
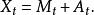 半鞅
半鞅其中M為一局部鞅,而A是一個右連左極的適應的有界變差過程。
右連左極函式
在數學中, 右連左極函式(càdlàg,RCLL)是指定義在實數集或其子集上的處處右連續且有左極限的函式。這類函式在研究有跳躍甚至是需要跳躍的隨機過程時很重要,這類隨機過程不像布朗運動具有連續的樣本軌道。給定定義域上的右連左極函式的集合稱為 斯科羅霍德空間(Skorokhod space)。全部連續函式都是右連左極函式。由累積分布函式的定義知所有的累積分布函式都是右連左極函式。
性質
•多個半鞅的線性組合仍然是半鞅。
•多個半鞅的積仍然是半鞅。
•任意半鞅的二次變差都存在。
•若X為一半鞅,f為二次連續可微函式,則f(X)也是半鞅。
例子
•凡是右連左極鞅都是半鞅,更一般地,上鞅和下鞅也都是半鞅。
•布朗運動是連續鞅,因此也是半鞅。
•適應並連續可微過程是有界變差過程,因此也是半鞅。
•萊維過程並不一定都是鞅,但一定都是半鞅。
布朗運動
布朗運動(Brownian motion)過程是一種常態分配的獨立增量連續隨機過程。它是隨機分析中基本概念之一。其基本性質為:布朗運動W(t)是期望為0、方差為t(時間)的正態隨機變數。對於任意的r小於等於s,W(t)-W(s)獨立於的W(r),且是期望為0、方差為t-s的正態隨機變數。可以證明布朗運動是馬爾可夫過程、鞅過程和伊藤過程。
它是在公元1827年英國植物學家羅伯特·布朗利用一般的顯微鏡觀察懸浮於水中由花粉所迸裂出之微粒時,發現微粒會呈現不規則狀的運動,因而稱它布朗運動。布朗運動也能測量原子的大小,因為就是有水中的水分子對微粒的碰撞產生的,而不規則的碰撞越明顯,就是原子越大,因此根據布朗運動,定義原子的直徑為10 厘米。
萊維過程
萊維過程(Lévy process)源於法國數學家保羅·皮埃爾·萊維,是連續時間上的一種擁有獨立穩定增量的左極限右連續(Càdlàg)的隨機過程。著名的例子有 Wiener過程和 泊松過程。
參見
•鞅
•局部鞅
•布朗運動
