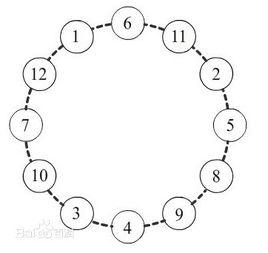
十二素數圈.問題
可以想像這種圈應該不止一個,其中一個示例解如下:
1 - 6 - 11 - 2 - 5 - 8 - 9 - 4 - 3 - 10 - 7 - 12 - (1).
現要求給出一種算法,來輸出任意一個或者多個解.如果無解則輸出"無解".
十二素數圈.算法
首先考慮12個自然數可以圍成多少個不同的圓圈.如果數量較少的話,就可以使用暴力搜尋來實現.因為是對稱的圓圈,任意一個數都可以放在首位(即,不存在實際意義上的首位).假設將1放在首位上,那么第2位上可以放11個不同的數字,第3位上可以放10個不同的數字...第12位上可以放1個數字.以此類推,不同的放法一共有 11*10*...*1 = (11!) 這么多種.再考慮重複的情況,實際上每種不同的做法都會被算上兩遍(左右對稱),那么真正不同的做法數量應該為: (11!) / 2 = 19958400.接近兩千萬,雖然一般的計算機還是可以承受的,但是實現起來需要使用11層循環,並且在問題的規模稍稍增長時,比如總數為14,循環的規模就會增長很多.可見這個方法太死,並且不夠實用.
比較實用的方法是,將這12個自然數構造成一個圖(Graph),將十二素數圈的構建轉換為圖的遍歷過程,這樣就能利用圖論中的搜尋和回溯理論來解決問題.
考慮第一個數的情況.如果第一個數為1,為了保證相鄰兩個數的和為素數,那么它附近(左邊和右邊)只能是2,4,6,10,12中的兩個,可見有效的選擇並不多.這樣就極大地限制了圖的規模,便於後面進行遍歷搜尋.現在考慮構建這個圖.將12個自然數看成是12個結點(Vertex),任意兩個數,如果其和為素數,那么就在它們之間設定一條路徑(Path),其長度即為兩數之和.在這裡,路徑的長度並沒有實際的意義,僅作為對路徑的一種標記.按這種方法構建的圖如下表所示(利用二維數組來存儲):
\圖論與回溯\圖的構建.jpg圖1. 用二維矩陣存儲的圖
可見這是一個非常稀疏的矩陣,並且是按照主對角線完全對稱的.
算法大概描述如下:
1. 任意選取一個結點放在素數圈的第一個位置上.以1為例子.
2. 在矩陣的第1行中順序搜尋有效路徑(即長度大於0的值),並將目標結點放置在素數圈的第二個位置上.例子中目標結點為2,路徑長度為3.
3. 刪掉與結點1相關的所有路徑(清零),包括第1行和第1列,都要清零,防止結點1再次被搜尋到.
4. 以結點2為當前結點,重複步驟2~3,直至素數圈的長度達到12.
5. 列印素數圈.一輪結束.
在這個過程中,最容易遇到也是最大的一個問題就是,如果遇到無解的情況怎么辦?這時就要使用回溯(Look Back Upon.百度的翻譯)的算法了.回溯就是回頭的意思.一條路走錯了,碰到死胡同了,當然要回頭,尋找前面曾經碰到過的岔路,去選擇另一條路試試看.這就是回溯算法的原理.
在這個例子中,有幾種情況需要回溯.
A. 碰到無解的情況.這是最常見的回溯條件.
B. 雖然能順次將12個結點都找到,但第12個結點與第1個結點之和不是素數.也即,這個圈的首尾不能相接.這也表示搜尋失敗.
C. 完成一個解的搜尋.因為我們的目標是找到所有解(或者一定數量的解),因此當完成一個解的時候,就需要回溯,繼續去尋找下一個解.
D. 遇到重複解.因為素數圈是完全對稱的,肯定會遇到重複解.這種情況需要捨棄.
歷史就在反覆的回溯中前進.如果有解,這種回溯的算法是一定可以找到它的,因為這本質上是一種深度優先的完全搜尋.找到所有解並依次列印出來,這個問題就解決了.
在具體實現中,回溯過程需要注意很多細節,其中一個就是路徑的恢復.由於前面一步走錯了,但是當時並不知道,就把走過的路徑都刪掉了,到回溯時就會發現有用的數據已經被自己無情地移除了.此時需要進行路徑的恢復工作.有兩種可行的方法.其一為記錄每次移除的路徑,回溯時連路徑一起回溯;其二為重新構建完整的路徑數據(重新生成原始圖),然後按照搜尋的完成進度來依次刪除前面用到過的路徑.後者實現比較簡單,但效率會稍低一點兒(整個搜尋過程中需要反覆地構建圖).本程式中偷一下懶,使用後者.
十二素數圈.代碼
十二素數圈圖2. 代碼截圖
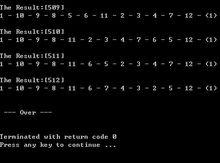\圖論與回溯\運行結果.jpg圖3. 運行結果的最後一部分
編譯環境: WinXP + MiniGW.
