區間分析

區間分析，又稱區間數學，是一門用區間變數代替點變數進行運算的數學分支。它最初是從計算數學的誤差理論研究發展起來的。1966年R.E.穆爾在《區間分析》一書中第一次系統提出區間運算理論。

區間分析

正文

又稱區間數學，是一門用區間變數代替點變數進行運算的數學分支。它最初是從計算數學的誤差理論研究發展起來的。1966年R.E.穆爾在《區間分析》一書中第一次系統提出區間運算理論。記I(R)為所有有限長區間總集合,即I(R)=｛【α,b)】│α≤b)，α，b)∈R｝，如果α=b)就是一個實數α=〔α,α〕稱為點區間,設I,J∈I(R)為兩區間，I=【α,b)】，J=【с,d】，可定義區間四則運算為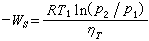

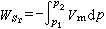
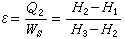
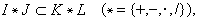
區間四則運算符合加法與乘法的交換律與結合律，但不符合乘法對加法分配律,而滿足次分配律,即對I,J，K∈I(R)有

符號I嶅J表示J包含I,I∩J表示區間之交，I∪J表示區間之並，它與集合運算規律相同。若I,J,K,L嶅I(R)且I嶅K,J嶅L則有

稱為區間運算的包含單調性。利用這一性質對任一有理函式ƒ(x)，可把點變數x換成區間變數x進行運算，這樣得到的區間值函式F稱為ƒ的區間擴展函式。
在n維空間中,若向量x＝(x1,x2,…,xn)的分量xj(i=1,2,…,n)都是區間，則x稱為n維區間向量，幾何上表示n維長方體。若n×m階矩陣A的元素Aij都是區間，則A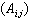＝ 稱為區間矩陣。對區間向量和矩陣也可定義它們的運算及範數。此外還可定義區間映射、區間導數、區間積分等等，它們構成區間分析的基本內容。將區間運算與其他數學領域相結合就形成了區間代數、區間幾何等等。
20世紀70年代以來區間數學有很大發展，在計算數學方面有很多套用，如利用區間疊代法可判斷對非線性方程組及運算元方程解的存在惟一性及區間疊代序列收斂性，這是點疊代法得不到的結果。此外，它在區間插值與逼近、線性方程、非線性規劃、微分方程等方面也有套用。直接用區間量計算的計算機語言──區間語言也已出現。
參考書目
　R. E. Moore,Interval Analysis,Prentice-Hall, Englewood Cliffs, New Jersey, 1966.

配圖

相關連線